题目内容
 一个半径为R的透明圆柱,其横截面积如图所示,该透明圆柱的折射率为
一个半径为R的透明圆柱,其横截面积如图所示,该透明圆柱的折射率为| 3 |
分析:画出光路图,由折射定律得到入射角与折射角的关系,由几何关系也得到入射角与折射角的关系,即可求出入射角与折射角,再根据几何知识求解这条入射光线到AB的距离.
解答: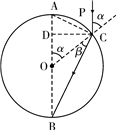 解:设光线P经C折射后过B点,光路如图所示.
解:设光线P经C折射后过B点,光路如图所示.
根据折射定律n=
=
①
在△OBC中,由几何关系得:α=2β ②
由①、②得:2cosβ=
③
可得β=30°,α=60° ④
所以CD=Rsin60°=
R ⑤
答:这条入射光线到AB的距离是
R.
 解:设光线P经C折射后过B点,光路如图所示.
解:设光线P经C折射后过B点,光路如图所示.根据折射定律n=
| sinα |
| sinβ |
| 3 |
在△OBC中,由几何关系得:α=2β ②
由①、②得:2cosβ=
| 3 |
可得β=30°,α=60° ④
所以CD=Rsin60°=
| ||
| 2 |
答:这条入射光线到AB的距离是
| ||
| 2 |
点评:对于几何光学问题,首先要正确作出光路图,其次要运用几何知识分析入射角与折射角的关系.

练习册系列答案
相关题目
 ,AB是圆的一条直径。现有一平行光沿AB方向射入圆柱体。其中一条光线经过一次折射后恰好经过B点,问:这条入射光线到AB的距离是多少?
,AB是圆的一条直径。现有一平行光沿AB方向射入圆柱体。其中一条光线经过一次折射后恰好经过B点,问:这条入射光线到AB的距离是多少?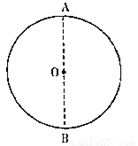

 一个半径为R的透明圆柱,其横截面积如图所示,该透明圆柱的折射率为
一个半径为R的透明圆柱,其横截面积如图所示,该透明圆柱的折射率为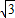 ,AB是圆的一条直径.现有一平行光沿AB方向射入圆柱体.其中一条光线经过一次折射后恰好经过B点,问:这条入射光线到AB的距离是多少?
,AB是圆的一条直径.现有一平行光沿AB方向射入圆柱体.其中一条光线经过一次折射后恰好经过B点,问:这条入射光线到AB的距离是多少?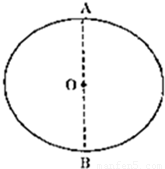 一个半径为R的透明圆柱,其横截面积如图所示,该透明圆柱的折射率为
一个半径为R的透明圆柱,其横截面积如图所示,该透明圆柱的折射率为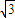 ,AB是圆的一条直径.现有一平行光沿AB方向射入圆柱体.其中一条光线经过一次折射后恰好经过B点,问:这条入射光线到AB的距离是多少?
,AB是圆的一条直径.现有一平行光沿AB方向射入圆柱体.其中一条光线经过一次折射后恰好经过B点,问:这条入射光线到AB的距离是多少?