题目内容
5.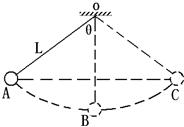 如图所示,把一个m=2kg的小球用细线悬挂起来,就成为一个摆,摆长为L=1m,将小球拉离最低点至最大偏角为θ=60°时让小球由静止开始自由摆动,如果阻力可以忽略,g=10m/s2.
如图所示,把一个m=2kg的小球用细线悬挂起来,就成为一个摆,摆长为L=1m,将小球拉离最低点至最大偏角为θ=60°时让小球由静止开始自由摆动,如果阻力可以忽略,g=10m/s2.(1)小球运动到最低点B时的速度是多大?
(2)摆至最低点B时,细线的拉力多大?
(3)摆至最低点B时,小球重力的瞬时功率是多大?
分析 小球在摆动的过程中,只有重力做功,机械能守恒,根据机械能守恒定律求出小球运动到最低位置时的速度大小.在最低点,小球靠重力和拉力的合力提供向心力,根据牛顿第二定律求出细线的拉力大小.由功率公式可求得重力的功率.
解答 解(1)由最大偏角θ处下落,到最低点时,竖直的高度差是h=l(1-cosθ)
有机械能守恒定律知
$\begin{array}{l}mgh=\frac{1}{2}m{v^2}\\ mgl({1-cosθ})=\frac{1}{2}m{v^2}\end{array}$
所以$v=\sqrt{2gl(1-cosθ)}$=$\sqrt{2×10×1×(1-0.5)}$=$\sqrt{10}$m/s
(2)在最低点合外力提供向心力
$\begin{array}{l}{F_合}={F_向}\\{F_拉}-G=\frac{{m{v^2}}}{l}\end{array}$
解得F拉=3mg-2mgcosθ=3×20-2×20×0.5=40N;
(3)最低点重力与速度相互垂直,故重力的功率为0;
答:(1)小球运动到最低位置时的速度是$\sqrt{10}$m/s.
(2)在最低点,细线的拉力为40N;
(3)重力的功率为0.
点评 本题综合考查了机械能守恒定律、向心力公式、功率及牛顿第二定律;要注意明确功率公式P=Fvcosθ的理解,当力和速度夹角为90度时,功率为零.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.一个质点分别受到下列四组共点力的作用,一定使质点产生加速度的一组共点力是( )
| A. | 25N,15N,40N | B. | 10N,15N,20N | C. | 10N,20N,40N | D. | 2N,4N,6N |
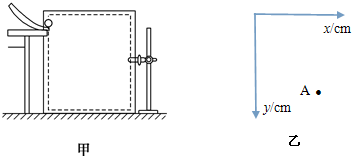
16.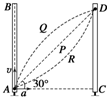 如图所示,竖直放置的两端封闭的玻璃管中注满清水,内有一个红蜡块能在水中以速度v匀速上浮.红蜡块从玻璃管的下端匀速上浮的同时,使玻璃管水平匀减速向右运动,则蜡块的轨迹可能是( )
如图所示,竖直放置的两端封闭的玻璃管中注满清水,内有一个红蜡块能在水中以速度v匀速上浮.红蜡块从玻璃管的下端匀速上浮的同时,使玻璃管水平匀减速向右运动,则蜡块的轨迹可能是( )
 如图所示,竖直放置的两端封闭的玻璃管中注满清水,内有一个红蜡块能在水中以速度v匀速上浮.红蜡块从玻璃管的下端匀速上浮的同时,使玻璃管水平匀减速向右运动,则蜡块的轨迹可能是( )
如图所示,竖直放置的两端封闭的玻璃管中注满清水,内有一个红蜡块能在水中以速度v匀速上浮.红蜡块从玻璃管的下端匀速上浮的同时,使玻璃管水平匀减速向右运动,则蜡块的轨迹可能是( )| A. | 直线P | B. | 曲线Q | C. | 曲线R | D. | 无法确定 |
20.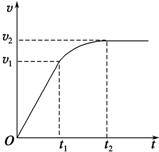 如图,为汽车在水平路面上启动过程的v-t图象.0~t1时间内为匀加速阶段,t1~t2时间内表示以额定功率行驶时的变加速阶段,t2后是与t轴平行的直线,设整个过程中汽车所受阻力恒定,则下列说法正确的是( )
如图,为汽车在水平路面上启动过程的v-t图象.0~t1时间内为匀加速阶段,t1~t2时间内表示以额定功率行驶时的变加速阶段,t2后是与t轴平行的直线,设整个过程中汽车所受阻力恒定,则下列说法正确的是( )
 如图,为汽车在水平路面上启动过程的v-t图象.0~t1时间内为匀加速阶段,t1~t2时间内表示以额定功率行驶时的变加速阶段,t2后是与t轴平行的直线,设整个过程中汽车所受阻力恒定,则下列说法正确的是( )
如图,为汽车在水平路面上启动过程的v-t图象.0~t1时间内为匀加速阶段,t1~t2时间内表示以额定功率行驶时的变加速阶段,t2后是与t轴平行的直线,设整个过程中汽车所受阻力恒定,则下列说法正确的是( )| A. | 0~t1时间内,牵引力增大,功率不变 | |
| B. | 0~t1时间内,牵引力为阻力的$\frac{{v}_{2}}{{v}_{1}}$倍 | |
| C. | 若v2=2v1,则0~t1时间内,牵引力做的功为mv12 | |
| D. | 若t2=2t1,则t1~t2时间内,牵引力做的功为mv22($\frac{{v}_{2}}{{v}_{2}-{v}_{1}}$) |
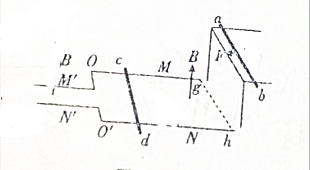 如图所示,水平金属导轨M,N宽L1=10cm,足够长的金属导轨M′,N′宽L2=5cm,它们用与导轨垂直的金属棒O,O′连接且处在方向竖直向上、磁感应强度B=10T的匀强磁场中,磁场的右边界为gh.金属棒cd垂直M,N静止在M、N导轨上,金属棒ab在光滑水平高台上受到大小为5N,方向水平向左的外力F的作用,作用时间t=0.4s,ab棒随后离开高台落至cd右侧的M,N轨上,M,N使ab棒竖直分速度变为0,但不影响ab棒的水平分速度,ab,cd棒始终平行且没有相碰.当cd,ab棒先后到达O、O′时,ab棒和cd棒均已经达到稳定速度,已知mab=mcd=m=1kg,不计一切摩擦阻力:求:
如图所示,水平金属导轨M,N宽L1=10cm,足够长的金属导轨M′,N′宽L2=5cm,它们用与导轨垂直的金属棒O,O′连接且处在方向竖直向上、磁感应强度B=10T的匀强磁场中,磁场的右边界为gh.金属棒cd垂直M,N静止在M、N导轨上,金属棒ab在光滑水平高台上受到大小为5N,方向水平向左的外力F的作用,作用时间t=0.4s,ab棒随后离开高台落至cd右侧的M,N轨上,M,N使ab棒竖直分速度变为0,但不影响ab棒的水平分速度,ab,cd棒始终平行且没有相碰.当cd,ab棒先后到达O、O′时,ab棒和cd棒均已经达到稳定速度,已知mab=mcd=m=1kg,不计一切摩擦阻力:求: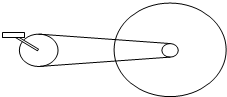 如图所示,是自行车传动结构的示意图,脚踏板与大齿轮共轴,大齿轮通过链条与小齿轮相连,后轮与小齿轮共轴,小齿轮带动后轮转动从而使自行车前进.假设脚踏板每t秒转一圈,已知自行车后轮半径为R,要知道这种情况下自行车的行驶速度,则
如图所示,是自行车传动结构的示意图,脚踏板与大齿轮共轴,大齿轮通过链条与小齿轮相连,后轮与小齿轮共轴,小齿轮带动后轮转动从而使自行车前进.假设脚踏板每t秒转一圈,已知自行车后轮半径为R,要知道这种情况下自行车的行驶速度,则
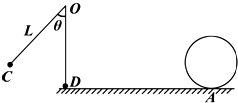 如图所示,让摆球从图中的C位置由静止开始摆下,摆到最低点D处,摆线刚好被拉断,小球在粗糙的水平面上由D点向右做匀减速运动,到达小孔进入半径R=0.25m的竖直放置的光滑圆弧轨道,当摆球进入圆轨道立即关闭A孔.已知摆线长L=2m,θ=60°,小球质量为m=1kg,D点与小孔A的水平距离s=2.5m,g取10m/s2.试求:
如图所示,让摆球从图中的C位置由静止开始摆下,摆到最低点D处,摆线刚好被拉断,小球在粗糙的水平面上由D点向右做匀减速运动,到达小孔进入半径R=0.25m的竖直放置的光滑圆弧轨道,当摆球进入圆轨道立即关闭A孔.已知摆线长L=2m,θ=60°,小球质量为m=1kg,D点与小孔A的水平距离s=2.5m,g取10m/s2.试求: