题目内容
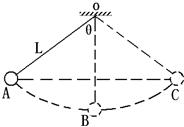
14.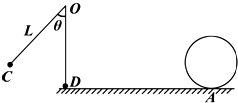 如图所示,让摆球从图中的C位置由静止开始摆下,摆到最低点D处,摆线刚好被拉断,小球在粗糙的水平面上由D点向右做匀减速运动,到达小孔进入半径R=0.25m的竖直放置的光滑圆弧轨道,当摆球进入圆轨道立即关闭A孔.已知摆线长L=2m,θ=60°,小球质量为m=1kg,D点与小孔A的水平距离s=2.5m,g取10m/s2.试求:
如图所示,让摆球从图中的C位置由静止开始摆下,摆到最低点D处,摆线刚好被拉断,小球在粗糙的水平面上由D点向右做匀减速运动,到达小孔进入半径R=0.25m的竖直放置的光滑圆弧轨道,当摆球进入圆轨道立即关闭A孔.已知摆线长L=2m,θ=60°,小球质量为m=1kg,D点与小孔A的水平距离s=2.5m,g取10m/s2.试求:(1)求摆线能承受的最大拉力为多大?
(2)要使摆球能进入圆轨道并且不脱离轨道,求摆球与粗糙水平面间的摩擦因数μ的范围.
分析 (1)摆球摆到D点时,摆线的拉力最大,根据机械能守恒定律求出摆球摆到D点时速度,由牛顿第二定律求出摆线的最大拉力.
(2)要使摆球能进入圆轨道,并且不脱离轨道,有两种情况:一种在圆心以下做等幅摆动;另一种能通过圆轨道做完整的圆周运动.
小球要刚好运动到A点,对小球从D到A的过程,运用动能定理求出动摩擦因数μ的最大值;
若小球进入A孔的速度较小,并且不脱离轨道,那么将会在圆心以下做等幅摆动,不脱离轨道,其临界情况为到达圆心等高处速度为零,根据机械能守恒和动能定理求出动摩擦因数.
要使摆球能进入圆轨道,恰好到达轨道的最高点,就刚好不脱离轨道,在最高点时,由重力提供向心力,由牛顿第二定律求出此时小球的速度,对从D到轨道最高点的过程,运用动能定理求解动摩擦因数的最小值,即可得到μ的范围.
解答 解:(1)当摆球由C到D运动,机械能守恒,则得:mg(L-Lcosθ)=$\frac{1}{2}m{v}_{D}^{2}$
在D点,由牛顿第二定律可得:Fm-mg=$\frac{m{v}_{D}^{2}}{L}$
联立可得:摆线的最大拉力为 Fm=2mg=10N
(2)小球不脱圆轨道分两种情况:
①要保证小球能达到A孔,设小球到达A孔的速度恰好为零,
对小球从D到A的过程,由动能定理可得:-μ1mgs=0-$\frac{1}{2}m{v}_{D}^{2}$
解得:μ1=0.5
若进入A孔的速度较小,那么将会在圆心以下做等幅摆动,不脱离轨道.其临界情况为到达圆心等高处速度为零,由机械能守恒可得:$\frac{1}{2}m{v}_{A}^{2}$=mgR
由动能定理可得:-μ2mgs=$\frac{1}{2}m{v}_{A}^{2}$-$\frac{1}{2}m{v}_{D}^{2}$
解得:μ2=0.35
②若小球能过圆轨道的最高点则不会脱离轨道,在圆周的最高点由牛顿第二定律可得:$mg=m\frac{v^2}{R}$
由动能定理可得:$-{μ_3}mgs-2mgR=\frac{1}{2}m{v^2}-\frac{1}{2}m{v_D}^2$
解得:μ3=0.125
综上,所以摩擦因数μ的范围为:0.35≤μ≤0.5或者0<μ≤0.125
答:(1)摆线能承受的最大拉力为10N;
(2)粗糙水平面摩擦因数μ的范围为:0.35≤μ≤0.5或者0<μ≤0.125.
点评 本题考查机械能守恒定律及动能定理、向心力公式等;关键是要全面分析不能漏解,要知道摆球能进入圆轨道不脱离轨道,有两种情况,再根据牛顿第二定律、机械能守恒和动能定理结合进行求解.

 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案| A. | 行星轨道的半长轴越长,自转周期就越小 | |
| B. | 行星轨道的半长轴越长,公转周期就越大 | |
| C. | 水星的半长轴最短,公转周期最大 | |
| D. | 海王星离太阳“最远”,其公转周期最小 |
| A. | 该行星的半径为$\frac{πvT}{2}$ | B. | 该行星的平均密度为$\frac{3π}{G{T}^{2}}$ | ||
| C. | 无法测出该行星的质量 | D. | 该行星表面的重力加速度为$\frac{2v}{T}$ |
| A. | 振幅一定为A | |
| B. | 速度的最大值一定为v | |
| C. | 开始振动的方向沿y轴向上或向下取决于它离波源的距离 | |
| D. | 若P点与波源距离s=vT,则质点P的位移与波源的相同 |
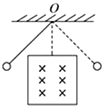 如图所示的圆形导体环用一根轻质细杆悬挂在O点,导体环可以在竖直平面里来回摆动,空气阻力和摩擦力均可不计.在如图所示的正方形区域里,有匀强磁场垂直于圆环的振动面指向纸内.下列说法中错误的是( )
如图所示的圆形导体环用一根轻质细杆悬挂在O点,导体环可以在竖直平面里来回摆动,空气阻力和摩擦力均可不计.在如图所示的正方形区域里,有匀强磁场垂直于圆环的振动面指向纸内.下列说法中错误的是( )| A. | 此摆振动的开始阶段机械能不守恒 | |
| B. | 导体环进入磁场和离开磁场时,环中电流的方向肯定相反 | |
| C. | 导体环通过最低点时,环中感应电流最大 | |
| D. | 最后此摆在匀强磁场中振动时,机械能守恒 |
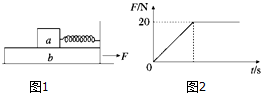
| A. | a与b始终保持相对静止 | |
| B. | a受到的摩擦力先减小、后增大再不变 | |
| C. | a受到的摩擦力先向左、后向右 | |
| D. | 当F=20N时,a受到的摩擦力为4N |
 如图所示,把一个m=2kg的小球用细线悬挂起来,就成为一个摆,摆长为L=1m,将小球拉离最低点至最大偏角为θ=60°时让小球由静止开始自由摆动,如果阻力可以忽略,g=10m/s2.
如图所示,把一个m=2kg的小球用细线悬挂起来,就成为一个摆,摆长为L=1m,将小球拉离最低点至最大偏角为θ=60°时让小球由静止开始自由摆动,如果阻力可以忽略,g=10m/s2.