题目内容
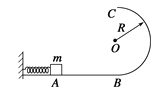
【题目】如图所示，质量为M表面光滑的斜面体放在粗糙的水平面上，其倾角为θ，斜面顶端与劲度系数为k自然长度为L的轻质弹簧相连，弹簧的下端连接着质量为m的物块。压缩弹簧使其长度为
时将物块由静止开始释放，且物块在以后的运动中斜面体始终处于静止状态，（重力加速度为g）则下列说法正确的是( )
A. 物块下滑的过程中弹簧的弹性势能一直增大
B. 物块下滑到速度最大时其重力势能减少
C. 物块下滑过程中，地面对斜面体的摩擦力最大值为
D. 斜面体与地面的摩擦因数
【答案】BD
【解析】因弹簧开始处于压缩状态，故当释放后物块下滑的过程中弹簧的弹性势能先减小后增大，选项A错误；根据平衡条件，处于平衡状态时：mgsinθ=k△x
得： 
，则物块下滑到速度最大时其重力势能减少
，选项B正确；
对斜面体而言，当物块到达最低点时地面对斜面体的摩擦力最大；物块作简谐运动的振幅为： 
；在平衡位置知，弹簧的伸长量为： 
；由对称性可知，最大伸长量为
= 
，选项C错误；
斜面体受力情况如图所示，由于斜面体平衡，所以有
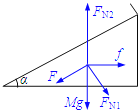
水平方向：f+FN1sinα-Fcosα=0
竖直方向：FN2-Mg-FN1cosα-Fsinα=0
又F=k（x+△L），FN1=mgcosα
联立可得：f=kxcosα，FN2=Mg+mg+kxsinα
为使斜面体始终处于静止，结合牛顿第三定律，应有|f|≤μFN2，所以 
当x=-A时，上式右端达到最大值，于是有
；选项D正确；故选BD.
练习册系列答案
相关题目
