题目内容
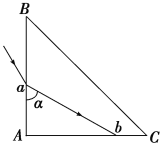
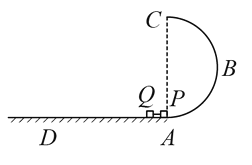
【题目】在竖直墙壁的左侧水平地面上,放置一个边长为![]() 、质量为
、质量为![]() 的正方体
的正方体![]() ,在墙壁和正方体之间放置一半径为
,在墙壁和正方体之间放置一半径为![]() 、质量为
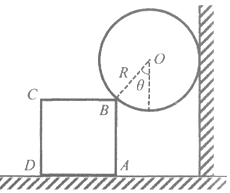
、质量为![]() 的光滑球,正方体和球均保持静止,如图所示。球的球心为
的光滑球,正方体和球均保持静止,如图所示。球的球心为![]() ,
,![]() 与竖直方向的夹角为
与竖直方向的夹角为![]() ,正方体的边长
,正方体的边长![]() ,正方体与水平地面的动摩擦因数为
,正方体与水平地面的动摩擦因数为![]() (已知重力加速度
(已知重力加速度![]() ,并认为最大静摩擦力等于滑动摩擦力)。求:
,并认为最大静摩擦力等于滑动摩擦力)。求:
(1)若![]() ,
,![]() ,竖直墙壁对球的弹力是多大?
,竖直墙壁对球的弹力是多大?
(2)若![]() ,保持球的半径不变,只增大球的质量,为了不让正方体出现滑动,则球质量的最大值为多少?(本问中取
,保持球的半径不变,只增大球的质量,为了不让正方体出现滑动,则球质量的最大值为多少?(本问中取![]() ,结果保留三位有效数字)。
,结果保留三位有效数字)。
(3)改变正方体到墙壁之间的距离,当正方体的右侧面![]() 到墙壁的距离小于某个值
到墙壁的距离小于某个值![]() 时,则无论球的质量是多少,球和正方体都始终处于静止状态,且球没有掉落地面,请问这个距离的值
时,则无论球的质量是多少,球和正方体都始终处于静止状态,且球没有掉落地面,请问这个距离的值![]() 是多少?
是多少?
【答案】(1)10N;(2)1.37kg;(3)1.5m
【解析】
(1)以球为研究对象,受力如图
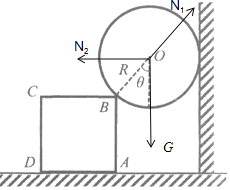
小球受力平衡,根据三角形定则可知,墙壁对球的弹力
![]()
(2)以正方体和球整体为研究对象,竖直方向受重力![]() 和地面的支持力
和地面的支持力![]() ,水平方向受墙壁的弹力
,水平方向受墙壁的弹力![]() 和地面的摩擦力
和地面的摩擦力![]() ,
,
根据平衡条件有
![]()
![]()
又因为
![]()
联立解得
![]()
所以球质量的最大值为![]() ;
;
(3)根据
![]()
![]()
![]()
得
![]()
所以
![]()
无论球的质量是多少都必须满足以上条件,则
![]()
得
![]()
故
![]()

练习册系列答案
相关题目