题目内容
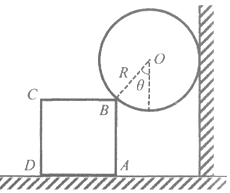
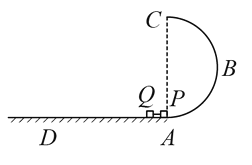
【题目】如图所示，竖直光滑的半圆轨道ABC固定在粗糙水平面上，直径AC竖直。小物块P和Q之间有一个被压缩后锁定的轻质弹簧，P、Q和弹簧作为一个系统可视为质点。开始时，系统位于4处，某时刻弹簧解锁（时间极短）使P、Q分离，Q沿水平面运动至D点静止，P沿半圆轨道运动并恰能通过最高点C，最终也落在D点。已知P的质量为m1=0.4kg，Q的质量为m2=0.8kg，半圆轨道半径R=0.4m，重力加速度g取l0m/s2，求：
（I）AD之间的距离；
（2）弹簧锁定时的弹性势能；
（3）Q与水平面之间的动摩擦因数。（结果保留两位小数）
【答案】（1）0. 8m （2）6J（3）0.31
【解析】
（1）设物块P在C点时的速度v，AD距离为L，由圆周运动和平抛运动规律，得
解得
（2）设P、Q分离瞬间的速度大小分别为
、
，弹簧锁定时的弹性势能为
，
由动量守恒定律和机械能守恒定律，得
联立解得
（3）设Q与水平面之间的动摩擦因数为
，由动能定理，得
解得
练习册系列答案
相关题目
