题目内容
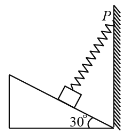
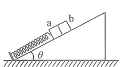
【题目】如图所示,两个均可视为质点且质量均为m=2kg的物块a和b放在倾角为![]() 的固定光滑且足够长的斜面上,在斜面底端和a之间固定连接有一根轻弹簧。现两物体处于静止状态,此时弹簧压缩量为x0=0.4m.从某时刻开始,对b施加沿斜面向上的外力,使b始终做匀加速直线运动。经过一段时间后,物块a、b分离;再经过同样长的时间,b到达轻弹簧的原长位置,弹簧的形变始终在弹性限度内,重力加速度为g=10m/s2,求
的固定光滑且足够长的斜面上,在斜面底端和a之间固定连接有一根轻弹簧。现两物体处于静止状态,此时弹簧压缩量为x0=0.4m.从某时刻开始,对b施加沿斜面向上的外力,使b始终做匀加速直线运动。经过一段时间后,物块a、b分离;再经过同样长的时间,b到达轻弹簧的原长位置,弹簧的形变始终在弹性限度内,重力加速度为g=10m/s2,求
(1)物块b加速度的大小;
(2)在物块a、b分离前,外力大小随时间变化的关系式;
(3)已知弹簧的弹性势能![]() (k为劲度系数,x指相对于原长的形变量),那么在a与b分离之后a还能沿斜面向上运动的距离。
(k为劲度系数,x指相对于原长的形变量),那么在a与b分离之后a还能沿斜面向上运动的距离。
【答案】(1)2.5m/s2;(2)![]() ;(3)
;(3)![]()
【解析】
(1)对整体分析,根据平衡条件可知
![]()
代入数据得
k=50N/m
由题意可知,b经两段相等时间的位移为x0,由匀变速直线运动位移与时间的关系![]() 可得第一阶段和第二阶段的位移分别为
可得第一阶段和第二阶段的位移分别为
![]() ,
,![]()
说明当形变量为![]() 时二者分离。
时二者分离。
对a分析,因分离时a与b间没有弹力,则根据牛顿第二定律可知
![]()
联立以上式子解得
![]()
(2)设时间为t,则经时间t时,a与b运动的位移
![]()
则形变量变为
![]()
对整体分析可知,由牛顿第二定律有
![]()
解得
![]()
因分离时位移![]() ,由
,由![]() 解得
解得
![]()
故应保证
![]()
F的表达式才能成立。
(3)在a与b分离之前a做匀变速运动,可得速度
![]()
设还能沿斜面往上运动x3的距离,依据能量守恒有
![]()
可得
![]()

练习册系列答案
相关题目