题目内容
【题目】在光滑的水平面上有一个质量为m=1kg的小球,小球一端与水平轻弹簧相连,另一端与和竖直方向成θ=600角不可伸长的轻绳相连,如图所示.此时小球处于静止状态,且水平面对小球的弹力恰好为零,当剪断轻绳的瞬间,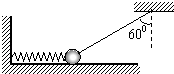
求:
(1)小球的加速度大小和方向.
(2)此时轻弹簧的弹力与水平面对小球的弹力的比值为多少?取g=10m∕s2 .
【答案】
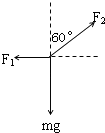
(1)解:由题意,小球处于静止状态,且水平面对小球的弹力恰好为零,以小球为研究对象,根据平衡条件得:
F1=F2sin60°
F2cos60°=mg
解得,F2=2mg,F1= ![]() mg
mg
当剪断轻绳瞬间弹簧的弹力大小不变,仍为 ![]() mg,小球在竖直方向上水平面支持力与重力平衡,根据牛顿第二定律得小球的加速度大小为:
mg,小球在竖直方向上水平面支持力与重力平衡,根据牛顿第二定律得小球的加速度大小为:
a= ![]() =
= ![]() g,方向水平向左.
g,方向水平向左.
答:小球的加速度大小为 ![]() g,方向水平向左
g,方向水平向左
(2)解:此时水平面对小球的弹力N=mg
故此时轻弹簧的弹力与水平面对小球的弹力的比值为F1:mg= ![]() mg:mg=
mg:mg= ![]()
答:此时轻弹簧的弹力与水平面对小球的弹力的比值为 ![]() .
.
【解析】(1)以小球为研究对象,根据题意,小球所受合力为零根据平衡条件列方程求出力的大小,剪断轻绳的瞬间,弹簧的弹力不变,根据牛顿第二运动定律,求出物体加速。
(2)对小球进行受力分析,借助三角形三边关系求出两个力之比。

练习册系列答案
相关题目