题目内容
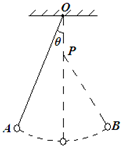 天花板上O点悬挂一单摆,绳子长度为0.99l,质量分布均匀的实心小球质量为m,直径为0.02l,O点正下方0.1l处有一钉子P,如图所示,现将单摆向左拉开一个小角度θ,并由静止释放,小球左右摆动过程中,偏角始终都小于5°,重力加速度为g.求:
天花板上O点悬挂一单摆,绳子长度为0.99l,质量分布均匀的实心小球质量为m,直径为0.02l,O点正下方0.1l处有一钉子P,如图所示,现将单摆向左拉开一个小角度θ,并由静止释放,小球左右摆动过程中,偏角始终都小于5°,重力加速度为g.求:(1)单摆的振动周期;
(2)小球从左摆到最低点时,绳子对小球的拉力大小.
分析:(1)根据单摆周期公式,结合题目条件,即可求解;
(2)根据机械能守恒定律与牛顿第二定律,即可求解.
(2)根据机械能守恒定律与牛顿第二定律,即可求解.
解答:解:(1)摆长OA的单摆周期:T1=2π
,
摆长PB的单摆周T2=2π
,
由题意得:l1=l
且l2=0.9l
单摆的振动周期:T=
解得:T=π
(1+
)
(2)从静止释放到最低点,由机械能守恒得
mv2=mgl(1-cosθ)
在最低点:T-mg=m
解得:T=mg(3-2cosθ)
答:(1)单摆的振动周期T=π
(1+
);
(2)小球从左摆到最低点时,绳子对小球的拉力大小mg(3-2cosθ).
|
摆长PB的单摆周T2=2π
|
由题意得:l1=l
且l2=0.9l
单摆的振动周期:T=
| T1+T2 |
| 2 |
解得:T=π
|
3
| ||
| 10 |
(2)从静止释放到最低点,由机械能守恒得
| 1 |
| 2 |
在最低点:T-mg=m
| v2 |
| l |
解得:T=mg(3-2cosθ)
答:(1)单摆的振动周期T=π
|
3
| ||
| 10 |
(2)小球从左摆到最低点时,绳子对小球的拉力大小mg(3-2cosθ).
点评:考查单摆周期公式与机械能守恒定律,及牛顿第二定律的应用,注意单摆摆长的变化,机械能守恒条件的判定.

练习册系列答案
相关题目
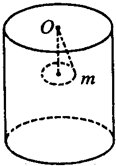 如图所示,在圆柱形房屋天花板中心O点悬挂一根长为L的细绳,绳的下端挂一个质量为m的小球,已知绳能承受的最大拉力为FT=2mg,小球在水平面内做圆周运动,当小球速度慢慢地逐渐增大到绳断裂后,小球恰好以速度v2=
如图所示,在圆柱形房屋天花板中心O点悬挂一根长为L的细绳,绳的下端挂一个质量为m的小球,已知绳能承受的最大拉力为FT=2mg,小球在水平面内做圆周运动,当小球速度慢慢地逐渐增大到绳断裂后,小球恰好以速度v2= 如图所示,在圆柱形房屋天花板中心O点悬挂一根长为L的细绳,绳的下端挂一个质量为m的小球,已知绳能承受的最大拉力为2mg,小球在水平面内做圆周运动,当速度逐渐增大到绳断裂后,小球恰好以速度v2=
如图所示,在圆柱形房屋天花板中心O点悬挂一根长为L的细绳,绳的下端挂一个质量为m的小球,已知绳能承受的最大拉力为2mg,小球在水平面内做圆周运动,当速度逐渐增大到绳断裂后,小球恰好以速度v2=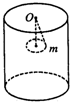 如图所示,在圆柱形房屋天花板中心O点悬挂一根长为L的细绳,绳的下端挂一个质量为m的小球,已知绳能承受的最大拉力为2mg,小球在水平面内做圆周运动,当速度逐渐增大到绳断裂后,小球恰好以速度v2=
如图所示,在圆柱形房屋天花板中心O点悬挂一根长为L的细绳,绳的下端挂一个质量为m的小球,已知绳能承受的最大拉力为2mg,小球在水平面内做圆周运动,当速度逐渐增大到绳断裂后,小球恰好以速度v2=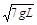 落到墙脚边.求
落到墙脚边.求