题目内容
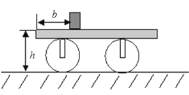
【题目】一平板车，质量 M=100kg，停在水平路面上，车身的平板离地面的高 度 h=1.25m，一质量 m=50kg 的物块置于车的平板上，它到车尾端的距离 b=1.00m， 与车板间的动摩擦因数μ =0.20。如图所示。今对平板车施一水平向右的恒力 F 使车向前行驶，结果物块从车板上滑落。物块刚离开车板的时刻，车向前行驶的 距离 s0=2.0m，不计路面与平板车间以及轮轴之间的摩擦，取 g=10m/s2。求：
（1）水平向右的恒力 F 的大小；
（2）物块落地时，落地点到车尾的水平距离 s。
【答案】（1）500N（2）1.625m
【解析】
（1）以m为研究对象进行分析，m在水平方向只受一个摩擦力f的作用，f=μmg，根据牛顿第二定律知
f=ma1
a1=μg=0.20×10m/s2=2m/s2
如图，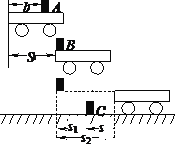
m从A点运动到B点，做匀加速直线运动，sAB=s0-b=1.00m，运动到B点的速度υB为：
物块在平板车上运动时间为
在相同时间里平板车向前行驶的距离s0=2.0m，则
所以平板车的加速度
此时平板车的速度为
v2=a2t1=4×1=4m/s
m从B处滑落时，以υB为初速度做平抛运动，落到C的水平距离为s1，下落时间为t2，则
s1=vBt2=2×0.5m=1.0 m
对平板车M，在m未滑落之前，水平方向受二力作用，即F和物块对平板车的摩擦力f，二者方向相反，平板车加速度为a2，由牛顿第二定律得：
F-f=Ma2
则有：
F=Ma2+f=（100×4+0.2×50×10）N=500N
（2）当m从平板车的B点滑落以后，平板车水平方向只受F作用，而做加速度为a3的匀加速运动，由牛顿第二定律得：
F=Ma3
即
在m从B滑落到C点的时间t=0.5s内，M运动距离s2为
物块落地时，落地点到车尾的水平距离s为
s=s2-s1=（2.625-1）m=1.625m
