题目内容
如图所示，竖直放置的两根足够长的光滑金属导轨相距为L，导轨的两端分别与电源（串有一滑动变阻器R）、定值电阻、电容器（原来不带电）和开关K相连。整个空间充满了垂直于导轨平面向外的匀强磁场，其磁感应强度的大小为B。一质量为m，电阻不计的金属棒ab横跨在导轨上。已知电源电动势为E，内阻为r，电容器的电容为C，定值电阻的阻值为R0，不计导轨的电阻。
（1）当K接1时，金属棒ab在磁场中恰好保持静止，则滑动变阻器接入电路的阻值R多大？
（2）当K接2后，金属棒ab从静止开始下落，下落距离s时达到稳定速度，则此稳定速度的大小为多大？下落s的过程中所需的时间为多少？
（3）先把开关K接通2，待ab达到稳定速度后，再将开关K接到3。试通过推导，说明ab棒此后的运动性质如何？求ab再下落距离s时，电容器储存的电能是多少？（设电容器不漏电，此时电容器还没有被击穿）
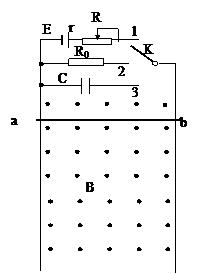
（1）
（2）
（3）“匀加速直线运动”，电流是恒定的 
解析:
（1）由
（1分） 
（1分）
得 （1分）
（2）由
（2分） 得
（1分）
由动量定理，得
（1分） 其中
=
（1分）
得
（1分） （或）
（3）K接3后的充电电流
（1分）
（1分） 得
=常数 （1分）
所以ab棒的运动性质是“匀加速直线运动”，电流是恒定的。（1分）
（1分），
根据能量转化与守恒得
（1分）
（1分） （或）
练习册系列答案
相关题目
如图所示，竖直放置的光滑圆环上套有一质量为m的小球，小球经过最高点时的速度为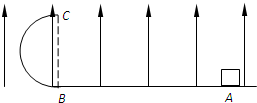
如图所示，竖直放置的半圆形绝缘轨道半径为R，下端与绝缘水平面平滑连接，整个装置处于方向竖直向上的匀强电场E中．一质量为m、带电量为+q的物块（可视为质点），从水平面上的A点以初速度v0水平向左运动，沿半圆形轨道恰好通过最高点C，场强大小
如图所示，竖直放置的轻弹簧一端固定在地面上，另一端与斜面体P固定，P与斜放的固定挡板MN接触且处于静止状态，则斜面体P此刻受到外力的个数可能是（ ）
物理选修3-3
如图所示，竖直放置的U形导轨宽为L，上端串有电阻R（其余导体部分的电阻都忽略不计）．磁感应强度为B的匀强磁场方向垂直于纸面向外．金属棒ab的质量为m，与导轨接触良好，不计摩擦．从静止释放后ab保持水平而下滑．试求