Question

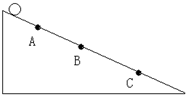
一小球从静止沿斜面以恒定的加速度滚下来，依次通过A、B、C三点，已知AB=12m，AC=32m，小球通过AB、BC所用的时间均为2s，则：
（1）求出小球下滑时的加速度？
（2）小球通过B点时的速度是多少？
（3）斜面A点以上部分至少有多长？

Answer 1

分析：（1）匀变速直线运动在相邻的相等时间内的位移之差是一恒量，根据△x=aT²求出小球下滑的加速度．
（2）某段时间内的平均速度等于中间时刻的瞬时速度，B点的速度等于AC段的平均速度．
（3）根据B点的速度，运用速度位移公式求出小球由静止运动到B点的位移，从而得出斜面A点以上的至少长度．

解答：解：（1）由△x=aT²得，a=

△x

T2

=

xBC-xAB

T2

=

20-12

4

m/s2=2m/s2．
答：小球下滑时的加速度为2m/s²．
（2）vB=

xAC

2T

=

32

4

m/s=8m/s
答：小球通过B点时的速度是8m/s．
（3）xOB=

vB2

2a

=

64

4

m=16m
则A点以上部分的长度x=x_OB-x_AB=4m
答：斜面A点以上部分至少4m．

点评：解决本题的关键掌握匀变速直线运动的推论，能够灵活运用推论进行求解．