题目内容
【题目】质量为M的小车置于水平面上．小车的上表面由 
圆弧和平面组成，车的右端固定有一不计质量的弹簧，圆弧AB部分光滑，半径为R，平面BC部分粗糙，长为l，C点右方的平面光滑．滑块质量为m，从圆弧最高处A无初速下滑（如图），与弹簧相接触并压缩弹簧，最后又返回到B相对于车静止．求：
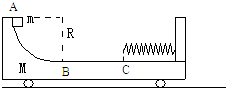
（1）BC部分的动摩擦因数μ；
（2）弹簧具有的最大弹性势能；
（3）当滑块与弹簧刚分离时滑块和小车的速度大小．
【答案】
（1）解：滑块与小车初始状态为静止，末状态滑块相对小车静止，即两者共速且速度为0，
据能量守恒：
mgR=μmg2l，
∴ 
答：BC部分的动摩擦因数 ；
（2）解：弹簧压缩到最大形变量时，滑块与小车又一次共速，且速度均为0，此时据能量守恒，
弹簧的弹性势能 
答：弹簧具有的最大弹性势能是 
；
（3）解：弹簧与滑块分离的时候，弹簧的弹性能为0，设此时滑块速度为v1，小车速度为v2据能量守恒有：
又因为系统动量守恒，有：mv1﹣Mv2=0
解得： 
答：当滑块与弹簧刚分离时滑块和小车的速度大小分别是 ， ．
【解析】（1）滑块与小车初始状态为静止，末状态滑块相对小车静止，即两者共速且速度为0，据能量守恒求解（2）弹簧压缩到最大形变量时，滑块与小车又一次共速，且速度均为0，据能量守恒求解．（3）弹簧与滑块分离的时候，弹簧的弹性能为0，据能量守恒和系统动量守恒求解．
【考点精析】根据题目的已知条件，利用功能关系和动量守恒定律的相关知识可以得到问题的答案，需要掌握当只有重力（或弹簧弹力）做功时，物体的机械能守恒；重力对物体做的功等于物体重力势能的减少:W G =E p1 -E p2；合外力对物体所做的功等于物体动能的变化:W 合 =E k2 -E k1 （动能定理）；除了重力（或弹簧弹力）之外的力对物体所做的功等于物体机械能的变化:W F =E 2 -E 1；动量守恒定律成立的条件：系统不受外力或系统所受外力的合力为零；系统所受的外力的合力虽不为零，但系统外力比内力小得多；系统所受外力的合力虽不为零，但在某个方向上的分量为零，则在该方向上系统的总动量的分量保持不变．
