题目内容
如图所示,在第一象限有一匀强电场,场强大小为E,方向与y轴平行;一质量为m、电荷量为-q(q>0)的粒子以平行于x轴的速度从y轴上P点处射入电场,已知OP=L,OQ=2 L.不计粒子重力.求:
L.不计粒子重力.求:
(1)粒子在第一象限中运动的时间.
(2)粒子离开第一象限时速度方向与x轴的夹角.
(1)  (2)30°
(2)30°
解析试题分析:
(1)带电粒子在电场中做类平抛运动,在y轴负方向上做初速度为零的匀加速运
动,设加速度的大小为a,在x轴正方向上做匀速直线运动,设速度为v0,粒子从P点
运动到Q点所用的时间为t,则由类平抛运动的规律可得:
l= at2 ,2
at2 ,2 l=v0t,且a=
l=v0t,且a=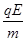
可得:t=
(2)设粒子射出第一象限时速度方向与x轴正方向的夹角为θ则tanθ=
解得tanθ= ,即θ=30°
,即θ=30°
考点:带电粒子在匀强电场中的运动、平抛

练习册系列答案
相关题目
如图所示的电路中,电源的电动势E和内阻r恒定不变,电灯L恰能正常发光,如果滑动变阻器的滑片向b端移动,则( )

| A.电灯L更亮,安培表的示数变大 |
| B.电灯L更亮,安培表的示数变小 |
| C.电灯L变暗,安培表的示数变小 |
| D.电灯L变亮,安培表的示数不变 |




