题目内容
【题目】宇宙中两颗相距较近的天体称为“双星”,它们以两者连线上的某一点为圆心做匀速圆周运动,而不至于因万有引力的作用吸引到一起。设二者的质量分别为m1和m2,两者相距为L,运动情景如图所示。求:
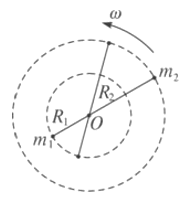
(1)双星的轨道半径之比;
(2)双星的线速度之比;
(3)双星的角速度。
【答案】(1)r1∶r2=m2∶m1;(2)v1∶v2=m2∶m1;(3)![]()
【解析】(1)在宇宙中的天体都绕着同一圆心做圆周运动,因此它们具有相同的角速度,且半径之和为L,即r1+r2=L.
天体m1做圆周运动时,天体m2对天体m1的万有引力提供m1做圆周运动的向心力,根据牛顿第二定律得: ![]()
同理可得天体m2做圆周运动时的向心力的表达式: ![]()
联立以上各式解得: r1∶r2=m2∶m1;
(2)又根据v=ωr得:v1∶v2=m2∶m1;
(3)根据r1∶r2=m2∶m1和r1+r2=L得: ![]() ,解得到
,解得到![]()

练习册系列答案
相关题目