题目内容
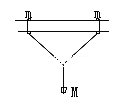
【题目】（18分）如图所示，光滑水平台面MN上放两个相同小物块A、B，右端N处与水平传送带理想连接，传送带水平部分长度L=8m，沿逆时针方向以恒定速度v0=2m/s匀速转动。物块A、B（大小不计，视作质点）与传送带间的动摩擦因数均为μ=0.2，物块A、B质量均为m=1kg。开始时A、B静止，A、B间压缩一轻质短弹簧。现解除锁定，弹簧弹开A、B，弹开后B滑上传送带，A掉落到地面上的Q点，已知水平台面高h=0.8m，Q点与水平台面间右端间的距离S=1.6m，g取10m/s2。
（1）求物块A脱离弹簧时速度的大小；
（2）求弹簧储存的弹性势能；
（3）求物块B在水平传送带上运动的时间。
【答案】（1）4m/s；（2）16J；（3）4.5s。
【解析】试题分析：（1）A作平抛运动，竖直方向：
（2分），水平方向：
（2分）
解得：vA=4m/s（1分）
（2）解锁过程系统动量守恒：
（2分）
由能量守恒定律：
（2分）
解得：Ep="16J" （1分）
（3）B作匀变速运动，由牛顿第二定律，
（1分）
解得：
（1分）
B向右匀减速至速度为零，由
，解得SB=4m＜L=8m，所以B最终回到水平台面。（1分）
设B向右匀减速的时间为t1：
（1分）
设B向左加速至与传送带共速的时间为t2，
（1分）
由
（1分），共速后做匀速运动的时间为t3：
（1分）
总时间：
（１分）
练习册系列答案
相关题目
