题目内容
 如图,一物体从光滑斜面AB底端A点以初速度v0上滑,沿斜面上升的最大高度为h.设下列情境中物体从A点上滑的初速度仍为v0,则下列说法中正确的是( )
如图,一物体从光滑斜面AB底端A点以初速度v0上滑,沿斜面上升的最大高度为h.设下列情境中物体从A点上滑的初速度仍为v0,则下列说法中正确的是( )分析:物体上升过程中只有重力做功,机械能守恒;斜抛运动运动最高点,速度不为零;AD轨道最高点,合力充当向心力,速度也不为零.
解答:解:A、若把斜面CB部分截去,物体冲过C点后做斜抛运动,由于物体机械能守恒,同时斜抛运动运动最高点,速度不为零,故不能到达h高处,故A错误;
B、若把斜面AB变成曲面AEB,物体在最高点速度为零,根据机械能守恒定律,物体沿此曲面上升仍能到达B点,故B正确;
C、若把斜面弯成圆弧形D,如果能到圆弧最高点,即h处,由于合力充当向心力,速度不为零,故会得到机械能增加,矛盾,故C错误;
D、若把斜面AB与水平面的夹角稍变大,物体在最高点速度为零,根据机械能守恒定律,物体沿斜面上升的最大高度仍然为h,故D错误;
故选B.
B、若把斜面AB变成曲面AEB,物体在最高点速度为零,根据机械能守恒定律,物体沿此曲面上升仍能到达B点,故B正确;
C、若把斜面弯成圆弧形D,如果能到圆弧最高点,即h处,由于合力充当向心力,速度不为零,故会得到机械能增加,矛盾,故C错误;
D、若把斜面AB与水平面的夹角稍变大,物体在最高点速度为零,根据机械能守恒定律,物体沿斜面上升的最大高度仍然为h,故D错误;
故选B.
点评:本题关键是根据机械能守恒定律分析,同时要知道斜抛运动和沿圆弧内侧运动到达最高点时,速度都不为零.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
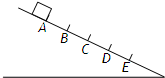 如图所示,一个小物体从光滑斜面上A点由静止开始下滑,在它通过的路程中取AE并分成相等的4段,即AB=BC=CD=DE,下列结论正确的是( )
如图所示,一个小物体从光滑斜面上A点由静止开始下滑,在它通过的路程中取AE并分成相等的4段,即AB=BC=CD=DE,下列结论正确的是( )A、物体到达各点的速率vB:vC:vD=vE=1:
| ||||||
B、物体到达各点所经历的时间tE=2tB=
| ||||||
| C、物体在BE段的平均速度等于CD段的平均速度 | ||||||
| D、物体通过每一段时,其速度增量相等 |
如图所示,一物体从光滑斜图AB底端A点以初速度 上滑,沿斜面上升的最大高度为h,下列说法中正确的是(设下列情境中物体从A点上滑的初速度仍为
上滑,沿斜面上升的最大高度为h,下列说法中正确的是(设下列情境中物体从A点上滑的初速度仍为 )( )
)( )
| A.若把斜面CB部分截去,物体冲过C点后上升的最大高度仍为h |
| B.若把斜面AB变成曲面AEB,物体沿此曲面上升仍能到达B点 |
| C.若把斜面弯成圆弧形D,物体仍沿圆弧升高h |
| D.若把斜面从C点以上部分弯成与C点相切的圆弧状,物体上升的最大高度有可能仍为h |
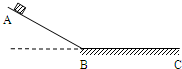 (2013?徐汇区一模)如图所示,t=0时,一小物体从光滑斜面上的A点由静止开始下滑,经过B点后进入水平面(设经过B点前后速度大小不变),最后停在C点.每隔2s测得的三个时刻物体的瞬时速度,记录在下表中.重力加速度g取10m/s2,则物体到达B点的速度为
(2013?徐汇区一模)如图所示,t=0时,一小物体从光滑斜面上的A点由静止开始下滑,经过B点后进入水平面(设经过B点前后速度大小不变),最后停在C点.每隔2s测得的三个时刻物体的瞬时速度,记录在下表中.重力加速度g取10m/s2,则物体到达B点的速度为 上滑,沿斜面上升的最大高度为h,下列说法中正确的是(设下列情境中物体从A点上滑的初速度仍为
上滑,沿斜面上升的最大高度为h,下列说法中正确的是(设下列情境中物体从A点上滑的初速度仍为
