题目内容
2.一根铁链长为L,放在光滑的水平桌面上,一端下垂,长度为a,若将链条由静止释放,则链条刚好离开桌子边缘时的速度大小为$\sqrt{\frac{{g({L^2}-{a^2})}}{L}}$.分析 铁链在运动的过程中,对整个铁链而言,机械能守恒.抓住系统重力势能的减小量等于动能的增加量,分别求出链条刚好离开桌面时的速度.
解答 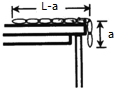 解:铁链释放之后,到离开桌面到落地的过程,由于桌面光滑,整个链条的机械能守恒.
解:铁链释放之后,到离开桌面到落地的过程,由于桌面光滑,整个链条的机械能守恒.
取桌面为零势能面,整个链条的质量为m.
根据机械能守恒定律得:
-$\frac{a}{L}$mg•$\frac{a}{2}$=$\frac{1}{2}$mv2-mg•$\frac{1}{2}$L
解得 v=$\sqrt{\frac{{g({L^2}-{a^2})}}{L}}$
故答案为:$\sqrt{\frac{{g({L^2}-{a^2})}}{L}}$.
点评 本题为机械能守恒定律应用的问题,要灵活选取零势能面,要注意链条不能看成质点,要研究重心的高度.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.某拱桥可以看成是一段圆弧,当汽车以10m/s的速度通过桥顶时,对桥顶的压力为车重的$\frac{3}{4}$倍,要使汽车对桥顶恰好没有压力,汽车的速度应为( )(g=10m/s2)
| A. | 15m/s | B. | 20m/s | C. | 25m/s | D. | 30m/s |
13.下列有关质点的说法中,正确的是( )
| A. | 当研究地球的自转时,可以将其看做质点 | |
| B. | 用GPS定位系统确定正在南极冰盖考察的某科考队员的位置时,该队员可看做质点 | |
| C. | 研究乒乓球在空中飞旋的轨迹时,不能将其看做质点 | |
| D. | 凡是小的物体,皆可看成质点;凡是大的物体,皆不能看成质点 |
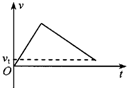
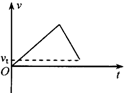
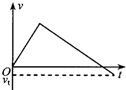
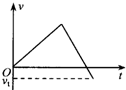
10.A、B两个物体在同一直线上运动,v-t图象如图,下列说法正确的是( )
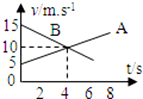

| A. | A、B运动方向相反 | |
| B. | A、B的加速度大小之比为1:1 | |
| C. | t=4s时,A、B的速度相同 | |
| D. | t=8s时A、B的速度分别为15m/s,5m/s |
17. 伽利略文理研究自由落体得有点规律,将落体实验转化为著名的“斜面实验”,对于这个研究过程,下列说法正确的是( )
伽利略文理研究自由落体得有点规律,将落体实验转化为著名的“斜面实验”,对于这个研究过程,下列说法正确的是( )
 伽利略文理研究自由落体得有点规律,将落体实验转化为著名的“斜面实验”,对于这个研究过程,下列说法正确的是( )
伽利略文理研究自由落体得有点规律,将落体实验转化为著名的“斜面实验”,对于这个研究过程,下列说法正确的是( )| A. | 斜面实验是一个理想实验 | |
| B. | 斜面实验放大了重力的作用,便于测量小球运动的路程 | |
| C. | 不直接做落体实验是因为当时时间测量不够精确 | |
| D. | 通过对斜面实验的观察与计算,直接得到落体运动的规律 |
7.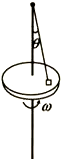 如图所示,水平转台上有一个质量为m的物块,用长为l的轻质细绳将物块连接在转轴上,细绳与竖直转轴的夹角θ为$\frac{π}{6}$,此时绳绷直但无张力,物块与转台间动摩擦因数为μ=$\frac{1}{3}$,最大静摩擦力等于滑动摩擦力,物块随转台由静止开始缓慢加速转动,角速度为ω 加速度为g,则( )
如图所示,水平转台上有一个质量为m的物块,用长为l的轻质细绳将物块连接在转轴上,细绳与竖直转轴的夹角θ为$\frac{π}{6}$,此时绳绷直但无张力,物块与转台间动摩擦因数为μ=$\frac{1}{3}$,最大静摩擦力等于滑动摩擦力,物块随转台由静止开始缓慢加速转动,角速度为ω 加速度为g,则( )
 如图所示,水平转台上有一个质量为m的物块,用长为l的轻质细绳将物块连接在转轴上,细绳与竖直转轴的夹角θ为$\frac{π}{6}$,此时绳绷直但无张力,物块与转台间动摩擦因数为μ=$\frac{1}{3}$,最大静摩擦力等于滑动摩擦力,物块随转台由静止开始缓慢加速转动,角速度为ω 加速度为g,则( )
如图所示,水平转台上有一个质量为m的物块,用长为l的轻质细绳将物块连接在转轴上,细绳与竖直转轴的夹角θ为$\frac{π}{6}$,此时绳绷直但无张力,物块与转台间动摩擦因数为μ=$\frac{1}{3}$,最大静摩擦力等于滑动摩擦力,物块随转台由静止开始缓慢加速转动,角速度为ω 加速度为g,则( )| A. | 当ω=$\sqrt{\frac{g}{2l}}$时,细线中张力为零 | |
| B. | 当ω=$\sqrt{\frac{3g}{4l}}$时,物块与转台间的摩擦力为零 | |
| C. | 当ω=$\sqrt{\frac{g}{l}}$时,细线的张力为$\frac{mg}{3}$ | |
| D. | 当ω=$\sqrt{\frac{4g}{3l}}$时,细绳的拉力大小为$\frac{4mg}{3}$ |
10.钴60(Co)是金属元素钴的放射性同位素之一,其半衰期为5.27年.它会通过β衰变放出能量高达315keV的高速电子衰变为镍60,同时会放出两束γ射线,其能量分别为1.17MeV及1.33MeV.钴60的应用非常广泛,几乎遍及各行各业.在农业上,常用于辐射育种、食品辐射保藏与保鲜等;在工业上,常用于无损探伤、辐射消毒、辐射加工、辐射处理废物以及自动控制等;在医学上,常用于癌和肿瘤的放射治疗.关于钴60,下列说法正确的是( )
| A. | 衰变方程为${\;}_{27}^{60}$Co→${\;}_{28}^{60}$Ni+${\;}_{-1}^{0}$e | |
| B. | 钴60衰变过程中不会有质量亏损 | |
| C. | 钴60可以作为示踪原子研究人体对药物的吸收 | |
| D. | 10g钴60经过15.81年还剩下1.25g钴60 |