Question

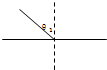一束光从空气射向折射率为

2

的某种玻璃的表面，如图所示，θ₁表示入射角，则下列说法中正确的是（　　）

• A、无论入射角θ₁有多大，折射角θ₂都不会超过45°角
• B、欲使折射角θ₂=30°，应以θ₁=45°角入射
• C、当入射角θ₁=arctan

  2

  时，反射光线与折射光线恰好互相垂直
• D、以上结论都不正确

Answer 1

分析：根据折射定律分析可知入射角最大时折射角也最大，并求出最大折射角的大小．结合几何关系，根据折射定律求出反射光线跟折射光线恰好垂直时入射角的大小．

解答：解：A、当入射角最大时，折射角最大，最大入射角为90°，根据折射定律得，n=

sin90°

sinβ

，解得最大折射角β=45°，所以折射角θ₂都不会超过45°角．故A正确．
B、折射角θ₂=30°时，根据折射定律得，n=

sinθ1

sinθ2

=

2

，解得：θ₁=45°．故B正确．
C、设入射角为α时，反射光线与折射光线垂直，此时反射角为i′=α，则折射角为r=90°-α，根据折射定律得，n=

sinα

sin90°-α)

=

2

，
解得：α=arctan

2

．故C正确．
D、由上可知D错误．
故选：ABC．

点评：解决本题的关键是掌握折射定律，并能根据折射定律分析出入射角最大时，折射角最大，并能求出最大折射角．