题目内容
选修题3-4
(1)一束光从空气射向折射率为
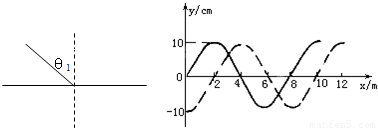
的某种玻璃的表面,如图甲所示,θ1表示入射角,则下列说法中不正确的是
A.无论入射角θ1有多大,折射角θ2都不会超过450角
B.欲使折射角θ2=300,应以θ1=450角入射
C.当入射角θ1=arctan
时,反射光线与折射光线恰好互相垂直
D.以上结论都不正确
(2).横波如图乙所示,t1时刻波形为图中实线所示;t2时刻波形如图中虚线所示.已知△t=t2-t1=0.5s,且3T<t2-t1<4T,问:
(1)如果波向右传播,波速多大?
(2)如果波向左传播,波速多大?

甲 乙.
(1)一束光从空气射向折射率为
| 2 |
A.无论入射角θ1有多大,折射角θ2都不会超过450角
B.欲使折射角θ2=300,应以θ1=450角入射
C.当入射角θ1=arctan
| 2 |
D.以上结论都不正确
(2).横波如图乙所示,t1时刻波形为图中实线所示;t2时刻波形如图中虚线所示.已知△t=t2-t1=0.5s,且3T<t2-t1<4T,问:
(1)如果波向右传播,波速多大?
(2)如果波向左传播,波速多大?

甲 乙.
分析:(1)光从空气射向玻璃时,当入射角接近90°时折射角最大,根据折射定律求出折射角的最大值.已知折射角,由折射定律求出入射角.
(2)由图读出波长.由已知条件3T<t2-t1<4T,根据波形的平移法,得出波传播的距离与波长的关系,求出波速.
(2)由图读出波长.由已知条件3T<t2-t1<4T,根据波形的平移法,得出波传播的距离与波长的关系,求出波速.
解答:解:(1)
A、入射角θ1≤90°,根据折射定律n=
得,sinθ2=
≤
=
,即θ2≤45°.故A正确.
B、当折射角θ2=30°时,由n=
解得,θ1=45°.故B正确.
C、当入射角θ1=arctan
时,由折射定律解得θ2=arccot
,根据数学知识得到arctan
+arccot
=90°,所以反射光线与折射光线恰好互相垂直.故C正确.
D、由上可知D错误.
本题选错误的,故选D
(2)
①简谐波在一个周期传播的距离是一个波长,如果波向右传播,3T<t2-t1<4T,则波传播的距离为△x=3
λ=
×8m=26m,波速为v=
=52m/s.
②如果波向左传播,波传播的距离为△x=3
λ=30m,波速为v=
=60m/s.
答:
(1)D;
(2)(1)如果波向右传播波速为52m/s;(2)如果波向左传播,波速为60m/s.
A、入射角θ1≤90°,根据折射定律n=
| sinθ1 |
| sinθ2 |
| sinθ1 |
| n |
| sin90° | ||
|
| ||
| 2 |
B、当折射角θ2=30°时,由n=
| sinθ1 |
| sinθ2 |
C、当入射角θ1=arctan
| 2 |
| 2 |
| 2 |
| 2 |
D、由上可知D错误.
本题选错误的,故选D
(2)
①简谐波在一个周期传播的距离是一个波长,如果波向右传播,3T<t2-t1<4T,则波传播的距离为△x=3
| 1 |
| 4 |
| 13 |
| 4 |
| △x |
| △t |
②如果波向左传播,波传播的距离为△x=3
| 3 |
| 4 |
| △x |
| △t |
答:
(1)D;
(2)(1)如果波向右传播波速为52m/s;(2)如果波向左传播,波速为60m/s.
点评:光的折射遵守折射定律,当光从疏介质射入光密介质时,入射角等于90°时,折射角最大.对于简谐波要抓住周期性,有时还要注意双向性.

练习册系列答案
相关题目








 注入人体,
注入人体,
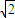 的某种玻璃的表面,如图甲所示,θ1表示入射角,则下列说法中不正确的是______
的某种玻璃的表面,如图甲所示,θ1表示入射角,则下列说法中不正确的是______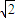 时,反射光线与折射光线恰好互相垂直
时,反射光线与折射光线恰好互相垂直