Question

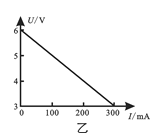
【题目】水平地面上有一固定的磁场斜面，倾角为，一质量滑块在平行于斜面向上的恒定拉力F作用下从静止开始沿斜面向上做匀加速度直线运动，滑块与斜面间的动摩擦因数。从滑块由静止开始运动时计时，在末撤去恒定拉力F，滑块刚好可以滑到斜面顶端，滑块在0到内图像如图乙所示，求：

（1）滑块前的加速度以及前内位移的大小；

（2）拉力F的大小；

（3）滑块经过斜面上距斜面顶点处所对应的时刻？

Answer 1

【答案】(1)8m(2)11N(3) 和

【解析】由v－t图像求出滑块前的加速度以及前内位移的大小，滑块在拉力作用下，由牛顿第二定律求出拉力F的大小，滑块先做匀加速直线运动，撤去力F后做匀减速运动，在沿斜面向下做匀加速运动，根据牛顿第二定律和运动学公式求出。

解：（1）由图可知：加速度大小

位移的大小即为图线与时间轴围成的面积： ；

（2）滑块在拉力作用下，受力分析如图：

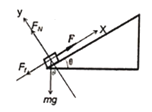
Y轴上，由平衡方程： ，

X轴上，由牛顿第二定律;

得到：

（3）滑块先以做匀加速直线运动，撤去力F后，滑块受力如图所示：

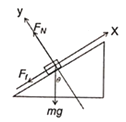
X轴上，由牛顿第二定律： ，得到：

以匀减速到0过程，位移

距顶端处的位置在减速前进的处。

由匀变速位移公式： ，解得： 或（已反向运动，舍弃）

得到：

所对应的时刻为

滑块减速到0时间为

此后滑块会下滑，摩擦力反向，设滑块加速度为

由牛顿第二定律：

解得：

设加速运动的时间为， ，得到：

所对应的时刻为：

即滑块经过斜面上距斜面顶点处所对应的时刻分别为和。