题目内容
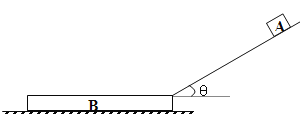
【题目】如图所示,一质量为![]() 的木板
的木板![]() 静止在光滑的水平面上,其右端上表面紧靠一固定斜面轨道的底端(斜面底端与木板
静止在光滑的水平面上,其右端上表面紧靠一固定斜面轨道的底端(斜面底端与木板![]() 右端的上表面之间有一段小圆弧平滑连接),轨道与水平面的夹角
右端的上表面之间有一段小圆弧平滑连接),轨道与水平面的夹角![]() ,一质量为
,一质量为![]() 的物块
的物块![]() 由斜面轨道上距轨道底端
由斜面轨道上距轨道底端![]() 处静止释放,物块
处静止释放,物块![]() 刚好没有从木板
刚好没有从木板![]() 的左端滑出,已知物块
的左端滑出,已知物块![]() 与斜面轨道间的动摩擦因数为0.25,与木板
与斜面轨道间的动摩擦因数为0.25,与木板![]() 上表面间的动摩擦因数为0.2,(
上表面间的动摩擦因数为0.2,(![]() ,
,![]() 取
取![]() )物块
)物块![]() 可看作质点。请问:
可看作质点。请问:
(1)物块![]() 刚滑上木板
刚滑上木板![]() 时的速度有多大?
时的速度有多大?
(2)物块![]() 从滑上木板
从滑上木板![]() 到相对木板
到相对木板![]() 静止经历了多长时间?
静止经历了多长时间?
(3)木板![]() 的长度
的长度![]() 为多少?
为多少?
【答案】(1)6m/s;.(2)2s;(3)6m.
【解析】
(1)对物体受力分析,物体做的是匀变速直线运动,由速度和位移的关系式可以求得末速度;
(2)物块A刚好没有从木板B左端滑出,说明此时它们的速度相等,由速度、位移公式可以求运行的时间;
(3)由匀变速规律可得AB的位移,两者位移之差为木板长度.
(1)物块A从斜面滑下时的加速度为:a1mAgsinθ-μ1mAgcosθ=mAa1
解得:a1=4m/s2
物块A刚滑上木板B时的速度为v1,有:v12v02=2a1s
解得:![]()
(2)物块A在木板B上滑动时,
A的加速度为:![]()
B的加速度为:![]()
经历时间t,两木块最终的共同速度为v2,所以:ν2=ν1+aAt=aBt
代入数据可解得:t=2s
(3)设木板B的长度为L,当两者共速时,木板B发生的位移为sB,物块A发生的位移为sA,根据题目所给条件可列方程:
sA=ν1t+![]() aAt2
aAt2
sB=![]() aBt2
aBt2
L=sA-sB
联立解得:L=6m

练习册系列答案
相关题目