题目内容
【题目】如图平面直角坐标系中,x轴上方区域存在垂直于纸面向里的匀强磁场,磁感应强度B=0.2T.原点O处有一粒子源,可在坐标平面内沿各个方向向磁场区发射比荷均为q/m=2.5×105C/kg的带负电的粒子.在x0=0.64m处垂直于x轴放置一块足够长的粒子收集板PQ,当粒子运动到收集板时即被吸收,不计粒子间相互作用和重力的影响,粒子被吸收的过程中收集板始终不带电.
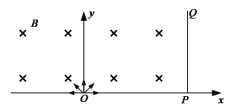
(1)能被收集的粒子速度至少多大?
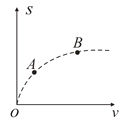
(2)设某时刻粒子源沿+y方向射入一系列粒子,速度大小从0到vm=2×104m/s不等,至少经多长时间有粒子到达收集板?求刚有粒子到达收集板时,该系列所有粒子所在位置构成的图线的方程;
(3)粒子源沿各个方向均匀地向磁场区发射速度大小均为vm=2×104m/s的粒子,会有两个不同方向入射的粒子在PQ上的同一位置被收集,求PQ上这种位置分布的区域长度,以及落在该区域的粒子占所发出粒子总数的百分比.
【答案】(1)![]() (2)
(2)![]()
![]() (3)
(3)![]() %
%
【解析】
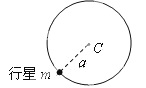
(1)如图1,在磁场中
![]()
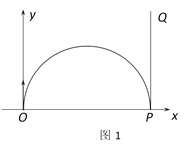
由题意,临界半径
![]()
联立可得
![]()
(2)速度为vm的粒子轨道半径为R,则:
![]()
解得:
R=0.4m
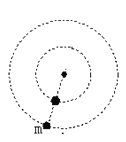
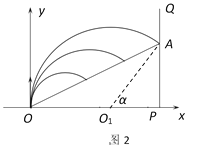
如图2,设该粒子击中A点,∠AO1P=α,有:
![]()
解得:
cosα=0.6
α=53°
所有粒子的圆周运动周期均为:
![]()
速度为vm的粒子转过圆心角为
180°-53°=127°
粒子到达收集板的最短时间:
![]()
此时这一系列的粒子位于线段OA上,其斜率为
![]()
所以图线方程为
![]()
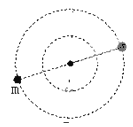
(3)临界1:如图3,初速度与+y轴成θ1的粒子轨迹直径与PQ交于M,这是PQ上离P最远的亮点。
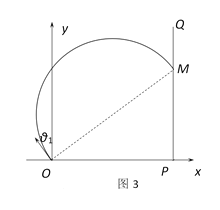
![]()
![]()
![]()
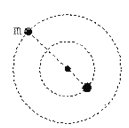
临界2:如图4,初速度与+y轴成θ2的粒子轨迹PQ相切于N,有![]() ,同(2),θ2=α=53°,说明N点与A点重合。
,同(2),θ2=α=53°,说明N点与A点重合。
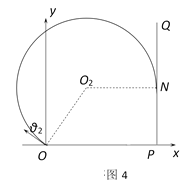
可得:
![]()
所求区域长度:
![]()
沿与+y轴成θ2=53°方向到+y方向发射的粒子均可以落在该区域,因此:
![]() %=
%=![]() %
%

 阅读快车系列答案
阅读快车系列答案