题目内容
(19分）如图，在倾角为37°的足够长的光滑斜面上，放一质量为mA=0.2kg的薄板A,A板上、下段由不同材料构成，下段表面光滑，长度l=3m，上段表面粗糙；质量为
的金属块B(视为质点）位于A的最下端,B与A上段间的动摩擦因数
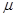=0.1；质量为
的物块C通过轻线绕过定滑轮与B相连。忽略滑轮质量及轴间的摩擦，A, B间最大静摩擦力可认为等于滑动摩擦力。开始时，整个系统在外力作用下，处子静止状态，轻线被拉直。
．求：
（1）撤去外力的瞬间，A, B, C的加速度分别是多大？
（2）撤去外力后的整个过程中，因摩擦产生的热量Q=？（绳足够长，B始终没滑出A板）
（1）
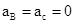
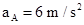（2）
【解析】
试题分析：（1）撤去外力前，C平衡则有绳子拉力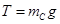
，B平衡则有绳子拉力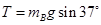
即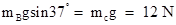
撤去外力的瞬间，BC的受力情况不变，所以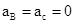
对薄板A，沿斜面方向有重力沿斜面向下的分力，没有摩擦力，所以又有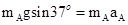
得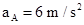
（2）由于斜面和A板下段表面都光滑，撤去外力后，A板从静止开始向下做匀加速运动，只要金属块B在A板下段表面上，B、C就保持静止不动。A板运动到金属块B在其上段表面上后，B和C受滑动摩擦力作用将一起以相同大小的加速度做加速运动。设A板上段刚滑到B下方时速度为vA，则
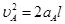
解得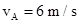
此过程无摩擦力，没有热量产生。
B在A板上端表面时，设A板加速度为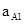
，B和C加速度为
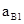，轻线拉力为
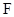，则
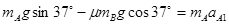
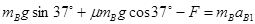
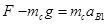
解得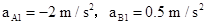
A、B、C最终达到速度相等。假设速度相等之后，A、B间的静摩擦力f小于最大静摩擦力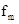
，即A、B相对静止，A、B、C三者加速度大小相同，设为
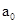，则
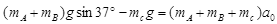
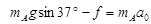
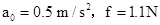
即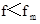
，假设成立，之后A、B相对静止。
设A、B、C达到相等速度v1所需时间为t，则
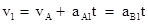
解得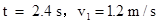
设在时间t内， A通过的距离是xA，B和C通过的距离是xB，则
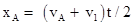
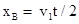
解得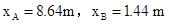
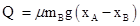
考点：功能关系 匀变速直线运动规律 受力分析 牛顿第二定律
如图，在倾角为θ的光滑斜面上，有两个用轻质弹簧相连接的物体A、B．它们的质量分别是mA和mB，弹簧的劲度系数k，C为一固定挡板．系统处于静止状态．现开始用一恒力F沿斜面方向拉物体A，使之沿斜面向上运动．若重力加速度为g，求：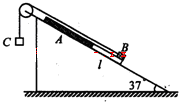
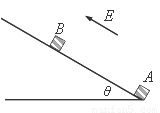
如图，在倾角为37°的足够长的光滑斜面上，放一质量为mA=0.2kg的薄板A，A板上、下段由不同材料构成，下段表面光滑，长度l=3m，上段表面粗糙；质量为mB=2.0kg的金属块B（视为质点）位于A的最下端，B与A上段间的动摩擦因数μ=0.1；质量为mC=1.2kg的物块C通过轻线绕过定滑轮与B相连．忽略滑轮质量及轴间的摩擦，A，B间最大静摩擦力可认为等于滑动摩擦力．开始时，整个系统在外力作用下，处子静止状态，轻线被拉
的足够长的光滑绝缘斜面上，带正电的物块A和不带电绝缘物块B相距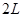
.
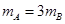，物块A位于斜面底端，斜面处于范围足够大、方向平行斜面向上的匀强电场中。将A、B同时由静止释放，两物块恰好在AB中点处发生第一次碰撞， A、B碰撞过程相互作用时间极短，已知A、B碰撞过程无机械能损失，且A的电荷没有转移，A、B均可视为质点，重力加速度为
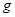。求： 
的足够长固定斜面上静置质量为
的小物块A，A与斜面间动摩擦因数
=tan
的光滑小物块B在斜面上与A相距为L处由静止释放，向A运动并与A正碰，碰撞时间极短，碰后A的速度为B碰前速度的
，求
