Question

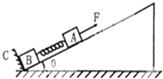
【题目】如图所示，在倾角为θ=37的固定光滑足够长斜面上有两个用轻弹簧相连接的物块A、B，它们的质量分别为m1=2kg、m2=3kg，弹簧劲度系数为k=100N/m，C为一固定挡板，系统处于静止状态。现用一平行于斜面向上的恒力F拉物块A使之向上运动，当物块B刚要离开挡板C时，物块A的速度为1m/s，加速度方向沿斜面向上，大小为0.5m/s2，已知sin37=0.6，cos37=0.8，g取10m/s2，则（ ）

A. 恒力F=31N

B. 从用力F拉物块A开始到B刚离开C的过程中，A沿斜面向上运动0.3m

C. 物块A沿斜面向上运动过程中，A先加速后匀速运动

D. A的速度达到最大时，B的加速度大小为0.5m/s2

Answer 1

【答案】AB

【解析】A、当B刚离开C时，B对挡板的弹力为零，有：kx2=m2gsinθ，解得弹簧的伸长量x2=m2gsinθk=3×10×0.6100m=0.18m，根据牛顿第二定律得，Fm1gsinθkx2=m1a，解得：F=31N，故A正确；

B、开始A处于静止状态，弹簧处于压缩，根据平衡有：m1gsinθ=kx1，解得弹簧的压缩量x1= m1gsinθ/k=2×10×0.6/100m=0.12m，可知从静止到B刚离开C的过程中，A发生的位移x=x1+x2=0.3m，故B正确；

C、对整体，根据牛顿第二定律可知F(m1+m2)gsinθ=(m1+m2)a，解得a=0.2 m/s2，故A不可能做匀速运动，故C错误；

D. 当A的加速度为零时，A的速度最大，设此时弹簧的拉力为FT，则：FFTm2gsinθ=0

所以FT=Fm2gsinθ=313×10×0.6N=13N，以B为研究对象,则：FTm2sinθ=ma′

所以：a′=0.75m/s2，故D错误。

故选：AB。