题目内容
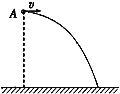
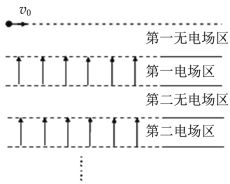
【题目】如图所示，在竖直平面内存在着两种区域：无电场区域和有理想上下边界的匀强电场区域。两种区域相互间隔，竖直高度相等均为h．电场区域共有n个，水平方向足够长，每一电场区域场强的大小均为E= 
，场强的方向均竖直向上。一个质量为m、电量为q的带正电小球(看作质点），从第一无电场区域的上边缘以初速度v0水平抛出，不计空气阻力，重力加速度为g ．则
（1）求小球刚离开第一个电场区域时的速度大小v1；
（2）求小球从开始运动到刚好离开第二个电场区域所经历的时间t2；
（3）若场强大小均为E= 
，方向不变，求小球从开始运动到刚好离开第n个电场区域所经历的总时间tn．
【答案】（1）
（2）
（3）
【解析】
(1)对小球应用动能定理可以求出小球离开第一个电场区域时的速度大小；
(2)根据题意求出小球的加速度，然后应用运动学公式求出小球的运动时间；
(3)根据小球的受力情况分析其运动过程，应用运动学公式求出小球经过第n个电场区域经历的总时间。
(1) 小球从开始运动到离开第一个电场区域过程，由动能定理得：mg2h-qEh=
解得：v1=
；
(2) 小球在第一个无电场区域内在竖直方向做自由落体运动，有：
解得：
小球离开第一个无电场区域时，在竖直方向分速度为：
小球进入第一个电场区域，在竖直方向做匀速直线运动，运动时间为：
小球在第二个无电场区域在竖直方向做匀加速直线运动，有：
解得：
小球离开第二个无电场区域时在竖直方向的分速度为：vy2=vy1+gt3=
小球进入第二个磁场区域在竖直方向做匀速直线运动，运动时间为：
小球从开始运动到刚好离开第二个电场区域所经历的时间为
t1=t1y+t2y+t3y+t3y=
；
(3) 小球在第一个无电场区域内在竖直方向做自由落体运动，有：
解得：
场强大小均为
小球在电场区域所受合力：qE-mg=mg，方向竖直向上
小球进入电场后在竖直方向做匀减速直线运动，离开电场时速度为零，
小球在第一个电场中的运动时间为：t2y=t1y=
小球在一个无电场区域与一个电场区域的总运动时间为：t=t1y+t2y=2
小球从开始运动到刚好离开第n个电场区域所经历的总时间为：tn=nt=2n。
