题目内容
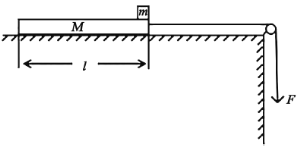
【题目】如图所示，长为l=24m、质量为M=2kg的长木板放在粗糙的水平平台上，质量为m=2kg（可看做质点）的物块放在长木板上表面的右端，在平台右侧边缘固定一定滑轮，绕过定滑轮的细线一端系在长木板上，连接长木板的细线始终保持水平，初始时物体均处于静止状态。现用大小为F=10N的拉力竖直向下拉细线，使长木板向右做加速运动，已知物块与长木板间的动摩擦因数
，长木板与平台的动摩擦因数
，且系统中物体所受最大静摩擦力等于滑动摩擦力，重力加速度g取10m/s2，长木板右端离定滑轮距离足够长，平台离地面足够高，求：
（1）在拉力F作用下，物块与长木板相对静止向右运动，此时它们之间的摩擦力大小；
（2）若不用拉力，而在细线上悬挂一个m′=2kg的重物，从静止释放重物m′以后，当物块相对于长木板滑行18m时，细线断开。则长木板从开始运动到停下来的整个过程中运动的时间。
【答案】（1）3N；（2）21s
【解析】
（1）当外力F作用时，假设M与m没有发生相对滑动，由牛顿第二定律可得
又滑动摩擦力为
代入数据a=1.5m/s2
则
假设成立，故
（2）由题可知，当悬挂上m′时，m与M已经发生相对滑动。此时令绳上的拉力为T，m的加速度a1，M的加速度为a2，细线断开时m的速度为Vm，M的速度为VM，细线断开后M的加速度为a3。对m′，m，M进行受力分析，由牛顿第二定律可得
代入数据，以上三式解得
，
假设经过时间
，两个物体相对运动的距离为
由
可得
代入数据，可得
细线断开时
，
细线断开后，由牛顿第二定律可知
解得
假设经过时间
，两个物体达到共速
由
可得
代入数据
，
在时间内，物块相对于木板的位移
故物块还在木板上。
由于
，两者保持相对静止，一直减速到零。根据牛顿第二定律，则有
继续运动的时间
所以整个运动的时间为
练习册系列答案
相关题目
