题目内容
 (1)一物体静止在水平面上,它的质量是m,与水平面之间的动摩擦因数为μ.用平行于水平面的力F分别拉物体,得到加速度a和拉力F的关系图象如图所示.利用图象可求出这个物体的质量m.
(1)一物体静止在水平面上,它的质量是m,与水平面之间的动摩擦因数为μ.用平行于水平面的力F分别拉物体,得到加速度a和拉力F的关系图象如图所示.利用图象可求出这个物体的质量m.甲同学分析的过程是:从图象中得到F=12N时,物体的加速度a=4m/s2,根据牛顿定律导出:m=
| F |
| a |
乙同学的分析过程是:从图象中得出直线的斜率为:k=tan45°=1,而K=
| 1 |
| m |
请判断甲、乙两个同学结论的对和错,并分析错误的原因.如果两个同学都错,分析各自的错误原因后再计算正确的结果.
(2)两颗靠得很近的天体,离其他天体非常遥远,靠相互吸引力一起以连线上某一点为圆心分别作圆周运动,从而保持两者之间的距离不变,这样的天体称为“双星’.现测得两星中心间距离为R,运动周期为T,求:双星的总质量.
解:设双星的质量分别为M1、M2.它们绕其连线上的O点以周期T作匀速圆周运动,由万有引力定律及牛顿第二定律得:G
| M1M2 |
| R2 |
| 2π |
| T |
| M1M2 |
| R2 |
| 2π |
| T |
请判断上述解法是否正确,若正确,请完成计算;若不正确,请说明理由,并用你自己的方法算出正确结果.
分析:(1)两位同学的分析都错误,甲错在把水平力F当作合外力,错在由于a轴和F轴的标度不同,斜率k不等于tan45°,正确解法是根据牛顿第二定律得出加速度与F的关系式,通过图线的斜率求出物体的质量.
(2)两星的转动半径不是R.靠相互间的万有引力提供向心力,做匀速圆周运动.抓住转动的周期相等,结合万有引力提供向心力,求出双子星的质量之和.
(2)两星的转动半径不是R.靠相互间的万有引力提供向心力,做匀速圆周运动.抓住转动的周期相等,结合万有引力提供向心力,求出双子星的质量之和.
解答:解:(1)甲、乙两同学的分析都错.
甲错在把水平力F当作合外力,而物块受摩擦力f=4N
乙错在由于a轴和F轴的标度不同,斜率k不等于tan45°
正确的求解是:由F-f=ma得:a=
F-f
K=
=0.5 m=2kg
(2)解法错误,两星的转动半径不是R.
正确的解法为:设两星转动半径分别为x与(R-x)G
=M1(
)2x
G
=M2(
)2(R-x)
联立解得:M1+M2=
答:(1)甲、乙两同学的分析都错. 甲错在把水平力F当作合外力,而物块受摩擦力f=4N 乙错在由于a轴和F轴的标度不同,斜率k不等于tan45°.物体的质量为2kg.
(2)双星的总质量为
.
甲错在把水平力F当作合外力,而物块受摩擦力f=4N
乙错在由于a轴和F轴的标度不同,斜率k不等于tan45°
正确的求解是:由F-f=ma得:a=
| 1 |
| m |
K=
| 1 |
| m |
(2)解法错误,两星的转动半径不是R.
正确的解法为:设两星转动半径分别为x与(R-x)G
| M1M2 |
| R2 |
| 2π |
| T |
G
| M1M2 |
| R2 |
| 2π |
| T |
联立解得:M1+M2=
| 4π2R3 |
| GT2 |
答:(1)甲、乙两同学的分析都错. 甲错在把水平力F当作合外力,而物块受摩擦力f=4N 乙错在由于a轴和F轴的标度不同,斜率k不等于tan45°.物体的质量为2kg.
(2)双星的总质量为
| 4π2R3 |
| GT2 |
点评:通过图线求解某些物理量时,我们往往的做法是得出图线的关系式,通过斜率、截距进行求解.
关于双星模型,知道其特点,抓住周期相等,靠相互间的万有引力提供向心力进行分析.
关于双星模型,知道其特点,抓住周期相等,靠相互间的万有引力提供向心力进行分析.

练习册系列答案
相关题目
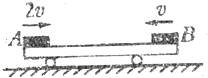 如图所示,一平板小车静止在光滑的水平面上,质量均为m的物体A、B分别以2v和v的初速度、沿同一直线同时从小车两端相向水平滑上小车.设两物体与小车间的动摩擦因数均为μ,小车质量也为m,最终物体A、B都停在小车上(若A、B相碰,碰后一定粘在一起)求:
如图所示,一平板小车静止在光滑的水平面上,质量均为m的物体A、B分别以2v和v的初速度、沿同一直线同时从小车两端相向水平滑上小车.设两物体与小车间的动摩擦因数均为μ,小车质量也为m,最终物体A、B都停在小车上(若A、B相碰,碰后一定粘在一起)求: (2011?庐阳区模拟)伽利略在《两种新科学的对话》一书中,讨论了自由落体运动和物体沿斜面运动的问题,提出了这样的猜想:物体沿斜面下滑是一种匀变速直线运动,同时他还运用实验验证了其猜想.合肥一中物理兴趣小组依据伽利略描述的实验方案,设计了如图所示的装置,探究物体沿斜面下滑是否做匀变速直线运动.
(2011?庐阳区模拟)伽利略在《两种新科学的对话》一书中,讨论了自由落体运动和物体沿斜面运动的问题,提出了这样的猜想:物体沿斜面下滑是一种匀变速直线运动,同时他还运用实验验证了其猜想.合肥一中物理兴趣小组依据伽利略描述的实验方案,设计了如图所示的装置,探究物体沿斜面下滑是否做匀变速直线运动. (2008?北京)有两个完全相同的小滑块A和B,A沿光滑水平面以速度v0与静止在平面边缘O点的B发生正碰,碰撞中无机械能损失.碰后B运动的轨迹为OD曲线,如图所示.
(2008?北京)有两个完全相同的小滑块A和B,A沿光滑水平面以速度v0与静止在平面边缘O点的B发生正碰,碰撞中无机械能损失.碰后B运动的轨迹为OD曲线,如图所示.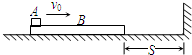 一质量M=2kg的长木板B静止在光滑的水平面上,B的右端与竖直挡板的距离为S=0.5m.一个质量为m=1kg的小物体A以初速度v0=6m/s从B的左端水平滑上B,当B与竖直挡板每次碰撞时,A都没有到达B的右端.
一质量M=2kg的长木板B静止在光滑的水平面上,B的右端与竖直挡板的距离为S=0.5m.一个质量为m=1kg的小物体A以初速度v0=6m/s从B的左端水平滑上B,当B与竖直挡板每次碰撞时,A都没有到达B的右端. (2012?上海模拟)在一次国际城市运动会中,要求运动员从高为H=4m的平台上A点由静止出发,沿着动摩擦因数为μ=0.2的滑道向下运动到B点后水平滑出,最后落在水池中.滑道的水平距离L大小不变,设滑道的水平距离为L=5m,B点的高度h可由运动员自由调节,A点不动,AB长度可以调整.(取g=10m/s2) 求:
(2012?上海模拟)在一次国际城市运动会中,要求运动员从高为H=4m的平台上A点由静止出发,沿着动摩擦因数为μ=0.2的滑道向下运动到B点后水平滑出,最后落在水池中.滑道的水平距离L大小不变,设滑道的水平距离为L=5m,B点的高度h可由运动员自由调节,A点不动,AB长度可以调整.(取g=10m/s2) 求: