题目内容
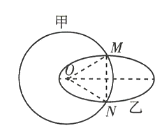
【题目】如图所示是宇宙空间中某处孤立天体系统的示意图，位于
点的一个中心天体有两颗环绕卫星，卫星质量远远小于中心天体质量，且不考虑两卫星间的万有引力。甲卫星绕点做半径为
的匀速圆周运动，乙卫星绕点的运动轨迹为椭圆，半长轴为、半短轴为
，甲、乙均沿顺时针方向运转。两卫星的运动轨迹共面且交于
两点。某时刻甲卫星在
处，乙卫星在
处。下列说法正确的是（ ）
A.甲、乙两卫星的周期相等
B.甲、乙两卫星各自经过处时的加速度大小相等
C.乙卫星经过处时速度相同
D.甲、乙各自从点运动到点所需时间之比为1：3
【答案】AB
【解析】
A．椭圆的半长轴与圆轨道的半径相等，根据开普勒第三定律知，两颗卫星的运动周期相等，故A正确；
B．甲、乙在
点都是由万有引力产生加速度，则有
故加速度大小相等，故B正确；
C．乙卫星在
两点的速度方向不同，故C错误；
D．甲卫星从到
，根据几何关系可知，经历
，而乙卫星从到经过远地点，根据开普勒行星运动定律，可知卫星在远地点运行慢，近地点运行快，故可知乙卫星从到运行时间大于
，而从到运行时间小于，故甲、乙各自从点运动到点的时间之比不是1：3，故D错误。
故选AB。
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
