题目内容
20.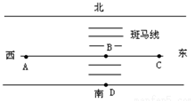 如图所示,在某市区,一辆小汽车在平直公路上向东匀速行驶,一位游客正由南向北从斑马线上匀速横穿马路,司机发现前方有危险(游客在D处),经0.3s作出反应后,在A点紧急刹车,仍将正步行至B处的游客撞伤,汽车最终停在C处,为了解现场,警方派一相同小车以法定最高速度vm=14m/s,行驶在同一路段,在肇事汽车的起始制动点A紧急刹车,经14m后停下来,现测得AB=17.5m、BC=14m、BD=2.6m,问:
如图所示,在某市区,一辆小汽车在平直公路上向东匀速行驶,一位游客正由南向北从斑马线上匀速横穿马路,司机发现前方有危险(游客在D处),经0.3s作出反应后,在A点紧急刹车,仍将正步行至B处的游客撞伤,汽车最终停在C处,为了解现场,警方派一相同小车以法定最高速度vm=14m/s,行驶在同一路段,在肇事汽车的起始制动点A紧急刹车,经14m后停下来,现测得AB=17.5m、BC=14m、BD=2.6m,问:(1)肇事汽车的初速度是多大?
(2)游客横穿马路的速度是多大?
分析 (1)警车从B到C过程,初末速度已知,位移已知,可以由位移速度关系式解得加速度,然后肇事车从A点刹车到C点停止,末速度、位移、加速度都是已知,再由位移速度关系式解出肇事车的初速度.
(2)根据位移速度关系式求出肇事汽车在出事点B的速度,再求出肇事汽车通过sAB段的平均速度,即可求出肇事汽车通过AB段的时间,由v=$\frac{x}{t}$求得游客横过马路的速度大小.
解答 解:(1)警车刹车后的加速度大小为a,则:$a=\frac{{v}_{m}^{2}}{2BC}$=$\frac{1{4}^{2}}{2×14}m/{s}^{2}$=7.0m/s2
因为警车行驶条件与肇事汽车相同,所以肇事汽车的加速度也为7.0m/s2,肇事汽车的速度为:
${v}_{A}=\sqrt{2a•AC}$=$\sqrt{2×7×31.5}m/s=21m/s$
(2)$AB={v}_{A}t-\frac{1}{2}a{t}^{2}$=17.5m,
代入数据解出:t=1.0s
游客的速度为:${v}_{人}=\frac{BD}{{t}_{1}+{t}_{2}}$=$\frac{2.6}{1+0.3}m/s=2m/s$
答:(1)肇事汽车的初速度是21m/s;
(2)游客横穿马路的速度是2m/s.
点评 在解决物理问题时,有时语言描述不好懂,我们可以结合图象更清晰直观的理解题目.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
10.在同一高度有两个小球同时开始运动,一个水平抛出,另一个自由落下,在它们运动过程中的每一时刻,有( )
| A. | 加速度不同,速度相同 | B. | 加速度相同,速度不同 | ||
| C. | 下落高度相同,位移不同 | D. | 下落高度不同,位移相同 |
8.要使平行板电容器的电容增大( )
| A. | 增大电容器的带电量 | B. | 增大电容器两极间的电压 | ||
| C. | 增大电容器两极板的距离 | D. | 增大电容器两极板的正对面积 |
12.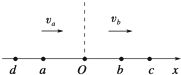 如图所示,弹簧振子在振动过程中,振子从a到b历时0.2s,振子经a、b两点时速度相同,若它从b再回到a的最短时间为0.4s,则该振子的振动频率为( )
如图所示,弹簧振子在振动过程中,振子从a到b历时0.2s,振子经a、b两点时速度相同,若它从b再回到a的最短时间为0.4s,则该振子的振动频率为( )
 如图所示,弹簧振子在振动过程中,振子从a到b历时0.2s,振子经a、b两点时速度相同,若它从b再回到a的最短时间为0.4s,则该振子的振动频率为( )
如图所示,弹簧振子在振动过程中,振子从a到b历时0.2s,振子经a、b两点时速度相同,若它从b再回到a的最短时间为0.4s,则该振子的振动频率为( )| A. | 1 Hz | B. | 1.25 Hz | C. | 2 Hz | D. | 2.5 Hz |
 如图所示,五块质量相同的木块,排放在光滑的水平面上,水平外力F作用在第一木块上,则第三木块对第四木块的作用力为F的$\frac{2}{5}$ 倍.
如图所示,五块质量相同的木块,排放在光滑的水平面上,水平外力F作用在第一木块上,则第三木块对第四木块的作用力为F的$\frac{2}{5}$ 倍. 如图所示是探究某根弹簧的伸长量x与所受拉力F之间的关系图,由图可知,弹簧的劲度系数是2000N/m;当弹簧受F=800N的拉力作用时,弹簧的伸长量为0.5cm.
如图所示是探究某根弹簧的伸长量x与所受拉力F之间的关系图,由图可知,弹簧的劲度系数是2000N/m;当弹簧受F=800N的拉力作用时,弹簧的伸长量为0.5cm. 在做“探究做功和物体速度变化关系”的实验前,某探究小组的同学们通过讨论提出了以下几种猜想:①W∝υ,②W∝υ2,③W∝$\sqrt{υ}$,….
在做“探究做功和物体速度变化关系”的实验前,某探究小组的同学们通过讨论提出了以下几种猜想:①W∝υ,②W∝υ2,③W∝$\sqrt{υ}$,….