Question

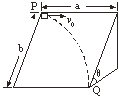
【题目】如图所示，倾角为30°的光滑斜面的下端有一水平传送带，传送带正以6m/s的速度运动，运动方向如图所示．一个质量为2kg的物体（物体可以视为质点），从h=3.2m高处由静止沿斜面下滑，物体经过A点时，不管是从斜面到传送带还是从传送带到斜面，都不计其动能损失．物体与传送带间的动摩擦因数为0.5，物体向左最多能滑到传送带左右两端AB的中点处，重力加速度g=10m/s2，求：

（1）传送带左右两端AB间的距离L．

（2）上述过程中物体与传送带组成的系统因摩擦产生的热量．

（3）物体随传送带向右运动，最后沿斜面上滑的最大高度h′．

Answer 1

【答案】（1）传送带左右两端AB间的距离为12.8 m；（2）上述过程中物体与传送带组成的系统因摩擦产生的热量为160 J；（3）物体随传送带向右运动，最后沿斜面上滑的最大高度h′为1.8m．

【解析】试题分析：（1）物体向左滑到AB的中点处时速度等于0，从静止开始到在传送带上的速度等于0的过程中运用动能定理即可求得L；

（2）物体与传送带组成的系统因摩擦产生的热量等于此过程中克服摩擦力所做的功，根据做功公式求出摩擦力所做的功；

（3）物体随传送带向右匀加速，要分析在到达A点前速度是否达到传送带的速度，如果达到，那就以传送带的速度冲上斜面，如果没有达到，就以匀加速直线运动的末速度冲上斜面，再根据动能定理即可求出最大高度．

（1）从静止开始到在传送带上的速度等于0的过程中运用动能定理得：

mgh﹣=0﹣0

解得：L="12.8" m．

（2）在此过程中，物体与传送带间的相对位移：

x相=+v带t

又=，

而摩擦热Q=μmgx相

以上三式可联立得Q="160" J．

（3）物体随传送带向右匀加速，当速度为v带="6" m/s时向右的位移为x，

则μmgx=

x="3.6" m＜，

即物体在到达A点前速度与传送带相等，最后以v带="6" m/s的速度冲上斜面，

由动能定理得：=mgh′

解得：h′="1.8" m．

答：（1）传送带左右两端AB间的距离为12.8 m；（2）上述过程中物体与传送带组成的系统因摩擦产生的热量为160 J；（3）物体随传送带向右运动，最后沿斜面上滑的最大高度h′为1.8m．