题目内容
 图中,轻弹簧的一端固定,另一端与滑块B相连,B静止在水平导轨上,弹簧处在原长状态.另一质量与B相同滑块A,从导轨上的P点以某一初速度向B滑行,当A滑过距离l1时,与B相碰,碰撞时间极短,碰后A、B紧贴在一起运动,但互不粘连.已知最后A恰好返回出发点P并停止.滑块A和B与导轨的滑动摩擦因数都为μ,运动过程中弹簧最大形变量为l2,求A从P出发时的初速度v0.
图中,轻弹簧的一端固定,另一端与滑块B相连,B静止在水平导轨上,弹簧处在原长状态.另一质量与B相同滑块A,从导轨上的P点以某一初速度向B滑行,当A滑过距离l1时,与B相碰,碰撞时间极短,碰后A、B紧贴在一起运动,但互不粘连.已知最后A恰好返回出发点P并停止.滑块A和B与导轨的滑动摩擦因数都为μ,运动过程中弹簧最大形变量为l2,求A从P出发时的初速度v0.分析:本题首先要将整个运动的过程分割成四个分过程,然后根据动能定律和动量守恒定律对各个分过程分别列式.
木块A运动到与木块B碰撞前,木块A做减速运动,只有摩擦力做功,可根据动能定理列方程;木块A与木块B碰撞过程,由于碰撞时间极短,内力远大于外力,系统动量守恒,可根据动量守恒定律列方程;木块A、B一起向左压缩弹簧再返回原处的过程,弹簧弹力做总功为零.只有摩擦力做功,再次根据动能定理列式;此后,由于木块B与弹簧相连,木块A、B会分离开,木块A恰好返回出发位置,对木块A运用动能定理列方程;最后联立以上各个方程求解即可.
木块A运动到与木块B碰撞前,木块A做减速运动,只有摩擦力做功,可根据动能定理列方程;木块A与木块B碰撞过程,由于碰撞时间极短,内力远大于外力,系统动量守恒,可根据动量守恒定律列方程;木块A、B一起向左压缩弹簧再返回原处的过程,弹簧弹力做总功为零.只有摩擦力做功,再次根据动能定理列式;此后,由于木块B与弹簧相连,木块A、B会分离开,木块A恰好返回出发位置,对木块A运用动能定理列方程;最后联立以上各个方程求解即可.
解答:解:令A、B质量皆为m,A刚接触B时速度为v1(碰前),由功能关系,有
-μmgl1=
m
-
m
①
A、B碰撞过程中动量守恒,令碰后A、B共同运动的速度为v2.有
mv1=2mv2 ②
碰后A、B先一起向左运动,接着A、B一起被弹回,在弹簧恢复到原长时,设A、B的共同速度为v3,在这过程中,弹簧势能始末两态都为零,利用功能关系,有
(2m)
-
(2m)
=μ(2m)g(2l2) ③
此后A、B开始分离,A单独向右滑到P点停下,由功能关系有
m
=μmgl1 ④
由以上各式,解得
v0=
即A从P出发时的初速度为
.
-μmgl1=
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 0 |
A、B碰撞过程中动量守恒,令碰后A、B共同运动的速度为v2.有
mv1=2mv2 ②
碰后A、B先一起向左运动,接着A、B一起被弹回,在弹簧恢复到原长时,设A、B的共同速度为v3,在这过程中,弹簧势能始末两态都为零,利用功能关系,有
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
| v | 2 3 |
此后A、B开始分离,A单独向右滑到P点停下,由功能关系有
| 1 |
| 2 |
| v | 2 3 |
由以上各式,解得
v0=
| μg(10l1+16l2) |
即A从P出发时的初速度为
| μg(10l1+16l2) |
点评:本题中除因木块与地面间的摩擦导致系统损失机械能外,两个木块的碰撞过程中系统也有机械能损失,由于碰撞过程的损失能量无法用碰撞力的功的形式直接求出来,故不能对整个过程运用动能定理列式,只有分段对各个过程运用动能定理和动量守恒定律列式,再分析求解.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案
相关题目
 如图所示,一轻弹簧固定于O点,另一端系一重物,将重物从与悬点O在同一水平面且轻弹簧保持原长的A点无初速度地释放,让它自由摆下,不计空气阻力,在重物由A点摆向最低点的过程中( )
如图所示,一轻弹簧固定于O点,另一端系一重物,将重物从与悬点O在同一水平面且轻弹簧保持原长的A点无初速度地释放,让它自由摆下,不计空气阻力,在重物由A点摆向最低点的过程中( )| A、重物的重力势能增加 | B、重力对重物一直做正功 | C、弹簧的弹性势能增加 | D、系统的机械能增加 |
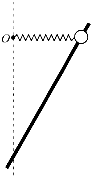 如图所示,质量为m的小球套在倾斜放置的固定光滑杆上,一根轻质弹簧一端固定于O点,另一端与小球相连,弹簧与杆在同一竖直平面内,将小球沿杆拉到弹簧水平位置由静止释放,小球沿杆下滑,当弹簧位于竖直位置时,小球速度恰好为零,此时小球下降的竖直高度为h,若全过程中弹簧始终处于伸长状态且处于弹性限度范围内,下列说法正确的是( )
如图所示,质量为m的小球套在倾斜放置的固定光滑杆上,一根轻质弹簧一端固定于O点,另一端与小球相连,弹簧与杆在同一竖直平面内,将小球沿杆拉到弹簧水平位置由静止释放,小球沿杆下滑,当弹簧位于竖直位置时,小球速度恰好为零,此时小球下降的竖直高度为h,若全过程中弹簧始终处于伸长状态且处于弹性限度范围内,下列说法正确的是( )| A、弹簧与杆垂直时,小球速度最大 | B、弹簧与杆垂直时,小球的动能与重力势能之和最大 | C、小球下滑至最低点的过程中,弹簧的弹性势能增加量小于mgh | D、小球下滑至最低点的过程中,弹簧的弹性势能增加量等于mgh |
 如图所示,质量mB=3.5kg的物体B通过一轻弹簧固连在地面上,弹簧的劲度系数k=100N/m.一轻绳一端与物体B连接,绕过无摩擦的两个轻质小定滑轮O1、O2后,另一端与套在光滑直杆顶端的、质量mA=1.6kg的小球A连接.已知直杆固定,杆长L为0.8m,且与水平面的夹角θ=37°.初始时使小球A静止不动,与A端相连的绳子保持水平,此时绳子中的张力F为45N.已知AO1=0.5m,重力加速度g取10m/s2,绳子不可伸长.现将小球A从静止释放,则:
如图所示,质量mB=3.5kg的物体B通过一轻弹簧固连在地面上,弹簧的劲度系数k=100N/m.一轻绳一端与物体B连接,绕过无摩擦的两个轻质小定滑轮O1、O2后,另一端与套在光滑直杆顶端的、质量mA=1.6kg的小球A连接.已知直杆固定,杆长L为0.8m,且与水平面的夹角θ=37°.初始时使小球A静止不动,与A端相连的绳子保持水平,此时绳子中的张力F为45N.已知AO1=0.5m,重力加速度g取10m/s2,绳子不可伸长.现将小球A从静止释放,则:
