题目内容
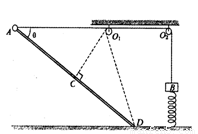
 如图所示,质量mB=3.5kg的物体B通过一轻弹簧固连在地面上,弹簧的劲度系数k=100N/m.一轻绳一端与物体B连接,绕过无摩擦的两个轻质小定滑轮O1、O2后,另一端与套在光滑直杆顶端的、质量mA=1.6kg的小球A连接.已知直杆固定,杆长L为0.8m,且与水平面的夹角θ=37°.初始时使小球A静止不动,与A端相连的绳子保持水平,此时绳子中的张力F为45N.已知AO1=0.5m,重力加速度g取10m/s2,绳子不可伸长.现将小球A从静止释放,则:
如图所示,质量mB=3.5kg的物体B通过一轻弹簧固连在地面上,弹簧的劲度系数k=100N/m.一轻绳一端与物体B连接,绕过无摩擦的两个轻质小定滑轮O1、O2后,另一端与套在光滑直杆顶端的、质量mA=1.6kg的小球A连接.已知直杆固定,杆长L为0.8m,且与水平面的夹角θ=37°.初始时使小球A静止不动,与A端相连的绳子保持水平,此时绳子中的张力F为45N.已知AO1=0.5m,重力加速度g取10m/s2,绳子不可伸长.现将小球A从静止释放,则:(1)在释放小球A之前弹簧的形变量;
(2)若直线CO1与杆垂直,求物体A运动到C点的过程中绳子拉力对物体A所做的功;
(3)求小球A运动到底端D点时的速度.
分析:(1)释放A球前,系统处于静止状态,隔离物体B便可求出弹簧的弹力,进而由胡克定律求得弹簧的形变量
(2)小球运动到C点的过程中,绳的拉力为变力,应用动能定理求解变力的功,同时考虑A、B、弹簧组成的相互作用的系统机械能守恒
(3)A球的下降过程,A、B、弹簧组成的相互作用的系统机械能守恒,注意A、B的速度之间的牵连关系,列出机械能守恒的方程可解.
(2)小球运动到C点的过程中,绳的拉力为变力,应用动能定理求解变力的功,同时考虑A、B、弹簧组成的相互作用的系统机械能守恒
(3)A球的下降过程,A、B、弹簧组成的相互作用的系统机械能守恒,注意A、B的速度之间的牵连关系,列出机械能守恒的方程可解.
解答:解:(1)释放小球前,B处于静止状态,由于绳子拉力大于重力,故弹簧被拉伸,设弹簧形变量为x有:
kx=F-mBg
所以,x=0.1m
(2)对A球从顶点运动到C的过程应用动能定理得:
W+mAgh=
mA
-0①
其中,h=xco1cos37°
而xco1=xAO1sin37°=0.3m
物体B下降的高度h′=xAO1-xco1=0.2m②
由此可知,弹簧此时被压缩了0.1m,此时弹簧弹性势能与初状态相等,对于A、B、和弹簧组成的系统机械能守恒:
mAgh+mBgh′=
mA
+
mB
③
由题意知,小球A运动方向与绳垂直,此瞬间B物体速度vB=0④
由①②③④得,W=7J
(3)由题意知,杆长L=0.8m,故∠CDO1=θ=37°
故DO1=AO1,当A到达D时,弹簧弹性势能与初状态相等,物体B又回到原位置,在D点对A的速度沿平行于绳和垂直于绳两方向进行分解,
可得,平行于绳方向的速度即为B的速度,由几何关系得:
=
cos37°⑤
对于整个下降过程由机械能守恒得:mAgLsin37°=
mA
+
mB
⑥
由⑤⑥得:
=2m/s
答:(1)弹簧形变量为0.1m
(2)绳子拉力对物体A所做的功7J
(3)小球A运动到底端D点时的速度为2m/s
kx=F-mBg
所以,x=0.1m
(2)对A球从顶点运动到C的过程应用动能定理得:
W+mAgh=
| 1 |
| 2 |
| v | 2 A |
其中,h=xco1cos37°
而xco1=xAO1sin37°=0.3m
物体B下降的高度h′=xAO1-xco1=0.2m②
由此可知,弹簧此时被压缩了0.1m,此时弹簧弹性势能与初状态相等,对于A、B、和弹簧组成的系统机械能守恒:
mAgh+mBgh′=
| 1 |
| 2 |
| v | 2 A |
| 1 |
| 2 |
| v | 2 B |
由题意知,小球A运动方向与绳垂直,此瞬间B物体速度vB=0④
由①②③④得,W=7J
(3)由题意知,杆长L=0.8m,故∠CDO1=θ=37°
故DO1=AO1,当A到达D时,弹簧弹性势能与初状态相等,物体B又回到原位置,在D点对A的速度沿平行于绳和垂直于绳两方向进行分解,
可得,平行于绳方向的速度即为B的速度,由几何关系得:
| v | ′ B |
| v | ′ A |
对于整个下降过程由机械能守恒得:mAgLsin37°=
| 1 |
| 2 |
| v | ′2 A |
| 1 |
| 2 |
| v | ′2 B |
由⑤⑥得:
| v | ′ A |
答:(1)弹簧形变量为0.1m
(2)绳子拉力对物体A所做的功7J
(3)小球A运动到底端D点时的速度为2m/s
点评:涉及弹簧的问题往往要向机械能守恒定律方向考虑,注意一个弹簧的弹性势能仅仅由其形变量决定,与是拉伸还是压缩无关;不在同一直线的连接体的运动,要运用运动的分解的办法解决两者的速度间的关系,往往将速度沿着绳的方向与垂直于绳的方向分解

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目