题目内容
一辆车箱长为L=2m的汽车，在平直的公路上以V0=36km/h的速度匀速行驶，车箱后挡板处放有一小木块，与车箱的动摩擦因数为μ=0.2，若汽车以大小为a=6m/s2的加速度刹车，求：（设木块对刹车没有影响，g取10m/s2）
（1）汽车从刹车到停止所用的时间？
（2）开始刹车后2s内，汽车的位移是多大？
（3）如果相对车箱而言，木块与车箱挡板碰撞时都以碰前的速率反弹．则从刹车起，木块经多长时间最终停下？
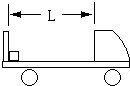
（1）汽车从刹车到停止所用的时间？
（2）开始刹车后2s内，汽车的位移是多大？
（3）如果相对车箱而言，木块与车箱挡板碰撞时都以碰前的速率反弹．则从刹车起，木块经多长时间最终停下？
v0=36km/h=10m/s
（1）从刹车起汽车停下所用时间：t0=
=
=1.67s
（2）2秒内汽车已经停止，所以汽车的位移为：s0=
=
=8.33m
（3）设从刹车起木块经时间t1后与前挡板相碰．
木块向前运动受滑动摩擦力，由牛顿第二定律得μmg=ma1
a1=μg=2m/s2
碰前木块的位移：s1=v0t1-
a1t12
碰前车的位移：s2=v0t1-
at12
另有s1-s2=L
解得t1=1s
碰前木块速度：v1=v0-a1t1=10-2×1m/s=8m/s
碰前汽车速度：v2=v0-at1=10-6×1m/s=4m/s
相对汽车，木块碰前速度为4m/s，碰后以4m/s的速度反弹．
相对地，碰后木块速度为0，在车厢摩擦力作用下将向前作匀加速直线运动，加速度大小仍为a1=2m/s2．
设又经时间t2木块的速度与汽车相等，则
木块速度：v1′=a1t2
汽车速度：v2′=v2-at2
因为v1′=v2′
所以t2=0.5s
v1′=v2′=1m/s
此时木块与前挡板距离为：L′=（v2t2-
at22）-
a1t22=1m
木块再经时间t3停下，则：t3=
=0.5s
木块再通过的位移为S3=
v1′t3=0.25m＜L′=1m不会与前板再碰．
而汽车再经时间t4=（t0-t1-t2）=0.17s停止运动，汽车先于木块停止运动．
木块运动的总时间：t=t1+t2+t3=2s
答：（1）汽车从刹车到停止所用的时间为1.67s；
（2）开始刹车后2s内，汽车的位移为8.33m；
（3）从刹车起，木块经2s最终停下．
（1）从刹车起汽车停下所用时间：t0=
| v0 |
| a |
| 10 |
| 6 |
（2）2秒内汽车已经停止，所以汽车的位移为：s0=
| v02 |
| 2a |
| 100 |
| 12 |
（3）设从刹车起木块经时间t1后与前挡板相碰．
木块向前运动受滑动摩擦力，由牛顿第二定律得μmg=ma1
a1=μg=2m/s2
碰前木块的位移：s1=v0t1-
| 1 |
| 2 |
碰前车的位移：s2=v0t1-
| 1 |
| 2 |
另有s1-s2=L
解得t1=1s
碰前木块速度：v1=v0-a1t1=10-2×1m/s=8m/s
碰前汽车速度：v2=v0-at1=10-6×1m/s=4m/s
相对汽车，木块碰前速度为4m/s，碰后以4m/s的速度反弹．
相对地，碰后木块速度为0，在车厢摩擦力作用下将向前作匀加速直线运动，加速度大小仍为a1=2m/s2．
设又经时间t2木块的速度与汽车相等，则
木块速度：v1′=a1t2
汽车速度：v2′=v2-at2
因为v1′=v2′
所以t2=0.5s
v1′=v2′=1m/s
此时木块与前挡板距离为：L′=（v2t2-
| 1 |
| 2 |
| 1 |
| 2 |
木块再经时间t3停下，则：t3=
| v1′ |
| a1 |
木块再通过的位移为S3=
| 1 |
| 2 |
而汽车再经时间t4=（t0-t1-t2）=0.17s停止运动，汽车先于木块停止运动．
木块运动的总时间：t=t1+t2+t3=2s
答：（1）汽车从刹车到停止所用的时间为1.67s；
（2）开始刹车后2s内，汽车的位移为8.33m；
（3）从刹车起，木块经2s最终停下．
练习册系列答案
相关题目
，求：
；
；
.