题目内容
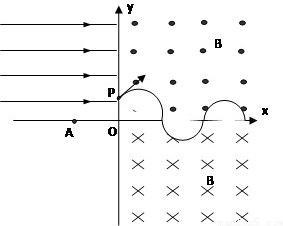
如图所示,真空中直角坐标系XOY,在第一象限内有垂直纸面向外的匀强磁场,在第四象限内有垂直纸面向里的匀强磁场,磁感应强度的大小均为B,在第二象限内有沿x轴正向的匀强电场,第三象限内有一对平行金属板M、N,两板间距为d.所加电压为U,两板间有垂直纸面向里、磁感应强度为B0的匀强磁场.一个正离子沿平行于金属板的轴线射入两板间并做直线运动,从A点(-L,0)垂直于x轴进入第二象限,从P(0,2L)进入第一象限,然后离子垂直于x轴离开第一象限,不计离子的重力,求:
(1)离子在金属板间运动速度V0的大小
(2)离子的比荷
(3)从离子进入第一象限开始计时,离子穿越x轴的时刻.

(1)离子在金属板间运动速度V0的大小
(2)离子的比荷
| q |
| m |
(3)从离子进入第一象限开始计时,离子穿越x轴的时刻.

(1)离子在板间做直线运动,电场力与洛伦兹力平衡
qE=qv0B0
E=
v0=
(2)离子在第二象限内做类平抛运动,离子在P点时沿y轴方向的分速度为v0,设沿x方向的分速度为vx
2L=v0t
L=
xt=
vxt
解得:vx=v0
离子在P点时的速度与y轴正方向成45°角
此时v=
v0
由几何关系可以确定离子在第一象限的轨道半径为:
r=2
L
根据qvB=m
可得
=
=
(3)离子在第一、第二象限内的轨迹如图所示:
离子的周期T=2π
=
离子第一次在第一象限内运动的时间t′=
T=
离子穿过x轴的时刻为t=n
+t′=(
+
)
n∈(0,1,2,…)
答:(1)离子在金属板间运动速度为
(2)离子的比荷为
=
(3)离子穿越x轴的时刻为(
+
)
n∈(0,1,2,…)
qE=qv0B0
E=
| U |
| d |
v0=
| U |
| B0d |
(2)离子在第二象限内做类平抛运动,离子在P点时沿y轴方向的分速度为v0,设沿x方向的分速度为vx
2L=v0t
L=
| . |
| v |
| 1 |
| 2 |
解得:vx=v0
离子在P点时的速度与y轴正方向成45°角
此时v=
| 2 |
由几何关系可以确定离子在第一象限的轨道半径为:
r=2
| 2 |
根据qvB=m
| v2 |
| r |
可得
| q |
| m |
| v |
| Br |
| U |
| 2BB0dL |
(3)离子在第一、第二象限内的轨迹如图所示:

离子的周期T=2π
| r |
| v |
| 4πB0dL |
| U |
离子第一次在第一象限内运动的时间t′=
| 3 |
| 8 |
| 3πB0dL |
| 2U |
离子穿过x轴的时刻为t=n
| T |
| 2 |
| n |
| 2 |
| 3 |
| 8 |
| 4πB0dL |
| U |
答:(1)离子在金属板间运动速度为
| U |
| B0d |
(2)离子的比荷为
| q |
| m |
| U |
| 2BB0dL |
(3)离子穿越x轴的时刻为(
| n |
| 2 |
| 3 |
| 8 |
| 4πB0dL |
| U |

练习册系列答案
相关题目