题目内容
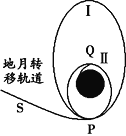
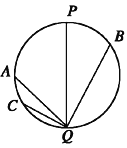
【题目】如图所示,PQ为圆的竖直直径,AQ、BQ、CQ为三个光滑斜面轨道,分别与圆相交于A、B、C三点。现让三个小球(可以看作质点)分别沿着AQ、BQ、CQ轨道自端点由静止滑下到Q点,运动的平均速度分别为v1、v2和v3。则有:
A. v2>v1>v3
B. v1>v2>v3
C. v3>v1>v2
D. v1>v3>v2
【答案】A
【解析】
设任一斜面的倾角为θ,圆槽直径为d,根据牛顿第二定律得出加速度与θ的关系,由运动学求出时间与θ和d的关系,由数学知识分析时间关系,然后分析平均速度.
设任一斜面的倾角为θ,圆槽直径为d。根据牛顿第二定律得到:a=gsinθ,斜面的长度为x=dsinθ,则有:x=![]() at2得
at2得![]() ,可见,物体下滑时间与斜面的倾角无关。则有t1=t2=t3。根据
,可见,物体下滑时间与斜面的倾角无关。则有t1=t2=t3。根据![]() 可知,因x2>x1>x3 ,可知v2>v1>v3,故选A.
可知,因x2>x1>x3 ,可知v2>v1>v3,故选A.

练习册系列答案
相关题目