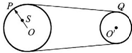如图所示.一个大轮通过皮带拉着小轮转动.皮带和两轮之间无滑动.大轮的半径是小轮的3倍.大轮上的一点s离转动轴的距离是半径的一半.P.S.Q三点的角速度之比=1:1:31:1:3,P.S.Q三点的线速度之比=2:1:22:1:2．题目和参考答案——青夏教育精英家教网—

题目内容

如图所示，一个大轮通过皮带拉着小轮转动，皮带和两轮之间无滑动，大轮的半径是小轮的3倍，大轮上的一点s离转动轴的距离是半径的一半，P、S、Q三点的角速度之比=

1：1：3

；P、S、Q三点的线速度之比=

2：1：2

．

分析：靠传送带传动轮子边缘上的点具有相同的线速度，共轴转动的点具有相同的角速度．根据v=rω，a=

和a=rω²可得出P、Q、S三点的角速度之比和向心加速度之比．

解答：解：P、Q两点的线速度相等，A的半径是B的半径的3倍，根据v=rω，知ω_P：ω_Q=1：3．P、S共轴转动，角速度相等，即ω_P：ω_S=1：1．所以ω_P：ω_S：ω_Q=1：1：3．
P、S、Q三点的半径之比为3：1.5：1=6：3：2，根据v=rω，P、S、Q三点的线速度之比为6：3：6=2：1：2．
故答案为：1：1：3；2：1：2．

点评：解决本题的关键知道靠传送带传动轮子边缘上的点具有相同的线速度，共轴转动的点具有相同的角速度．掌握线速度与角速度的关系，以及线速度、角速度与向心加速度的关系．

练习册系列答案

单元测试AB卷吉林出版集团有限责任公司系列答案

相关题目

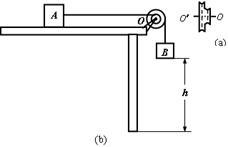
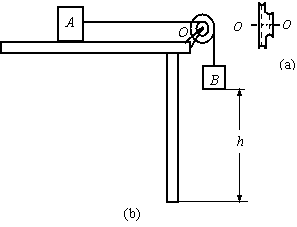
线轮的两部分半径不同（其侧视图如图a所示），大轮半径R=10cm，小轮半径r=5cm．线轮可绕固定支架上的光滑水平轴OO′转动，小轮通过细绳与放在水平桌面上的物体A相连，大轮通过细线与物体B相连，如图b所示．A、B质量分别为m_A=4kg、m_B=0.75kg，A与桌面间的动摩擦因数μ=0.5，B的下表面距地面高h=1m．不计细绳和线轮的质量，整个系统处于静止状态．（g=10m/s²）求：
（1）物体A所受到的静摩擦力大小．
（2）将物体B换成一个大小相同，质量为原来两倍的物体B′后，整个系统由静止开始运动，当物体B′落到地面的瞬间，物体A的速度大小．
（3）在（2）描述的情况下，B′从开始运动至落地的时间．

线轮的两部分半径不同（其侧视图如图a所示），大轮半径R＝10cm，小轮半径r＝5cm。线轮可绕固定支架上的光滑水平轴OO′转动，小轮通过细绳与放在水平桌面上的物体A相连，大轮通过细线与物体B相连，如图b所示。A、B质量分别为m_A＝4kg、m_B＝0.75kg，A与桌面间的动摩擦因数μ=0.5，B的下表面距地面高h＝1m。不计细绳和线轮的质量，整个系统处于静止状态。（g=10m/s²）求：

（1）物体A所受到的静摩擦力大小。

（2）将物体B换成一个大小相同，质量为原来两倍的物体B′后，整个系统由静止开始运动，当物体B′落到地面的瞬间，物体A的速度大小。

（3）在（2）描述的情况下，B′从开始运动至落地的时间。

线轮的两部分半径不同（其侧视图如图a所示），大轮半径R＝10cm，小轮半径r＝5cm。线轮可绕固定支架上的光滑水平轴OO′转动，小轮通过细绳与放在水平桌面上的物体A相连，大轮通过细线与物体B相连，如图b所示。A、B质量分别为m_A＝4kg、m_B＝0.75kg，A与桌面间的动摩擦因数μ=0.5，B的下表面距地面高h＝1m。不计细绳和线轮的质量，整个系统处于静止状态。（g=10m/s²）求：
⑴物体A所受到的静摩擦力大小。
⑵将物体B换成一个大小相同，质量为原来两倍的物体B′后，整个系统由静止开始运动，当物体B′落到地面的瞬间，物体A的速度大小。
⑶在⑵描述的情况下，B′从开始运动至落地的时间。

试题分类