题目内容
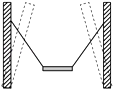
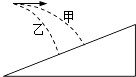
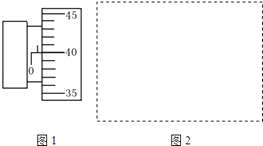
【题目】如图甲所示，竖直平面内的平面直角坐标系xoy，y轴竖直向上，第三象限梯形OACD范围内加有竖直向上的匀强电场和垂直纸面向里的匀强磁场B，电场强度为E1=1.5N/C，B大小未知；OA与y轴成θ=45°夹角．第三、四象限在梯形之外加有水平方向的电场E2 ， 其大小随时间变化如图乙所示（取水平向右为正向）．今有带电小球从A点正上方的F点（x=﹣0.15 
m，y=0.1m）自由下落，在梯形中恰做匀速圆周运动，t=0时刻恰垂直于OA边进入E2的电场中，t1时刻第一次经过y轴，t2时刻第二次经过y轴．（g=10m/s2）求：
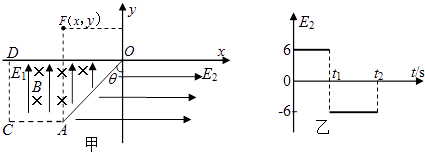
（1）磁感应强度B的大小；
（2）小球在磁场中运动的时间；
（3）时刻t1、t2各为多少．
【答案】
（1）
解：小球在梯形中恰做匀速圆周运动，电场力和重力相等，则有：qE1=mg，
解得： 
；
小球进入复合场中的速度为v，根据自由落体运动可得：mgy= 
，
代入数据解得：v= 
；
根据题意可知，粒子在复合场中做圆周运动的半径为：R=x=0.15 
m，
根据洛伦兹力提供向心力可得：qvB=m 
，
联立并代入数据解得：B=1T
（2）
解：小球在磁场中运动的圆心即为O，轨迹对应的圆心角为： 
，
所以小球在磁场中运动时间为：t= 
≈0.12s
（3）
解：粒子射出复合场后沿水平方向的分速度为：vx=vcos45°=1m/s，
设水平方向的加速度大小为a，根据牛顿第二定律可得： 
，
小球离开磁场时距离y轴的距离为： 
，
根据位移时间关系可得： 
，
代入数据解得：t1=0.065s；
第一次经过y轴时水平方向的速度为：v1=vx+at1=（1+40×0.065）m/s=3.6m/s，
粒子再次回到y轴的时间为：t′1= 
，
所以有：t2=t1+t′1=0.065s+0.18s=0.245s
【解析】（1）根据电场力和重力相等求解比荷，根据自由落体运动求出进入磁场中的速度，根据几何关系求解半径，再根据洛伦兹力提供向心力求解磁感应强度；（2）求出小球在磁场中运动轨迹对应的圆心角，根据周期公式求解时间；（3）水平方向根据牛顿第二定律求解加速度，再根据位移时间关系、速度时间关系求解时间．
【考点精析】本题主要考查了向心力和洛伦兹力的相关知识点，需要掌握向心力总是指向圆心，产生向心加速度，向心力只改变线速度的方向，不改变速度的大小；向心力是根据力的效果命名的.在分析做圆周运动的质点受力情况时，千万不可在物体受力之外再添加一个向心力；洛伦兹力始终垂直于v的方向，所以洛伦兹力一定不做功才能正确解答此题．
