��Ŀ����
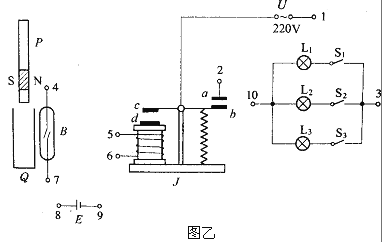
����Ŀ����ͼ��ʾ��ˮƽ�����Ϲ̶���һU�ν�������MNPQ �� ����������ֱ����ǿ�ų��У���һ�����ab�ڵ��������������˶���������뵼��ʼ�սӴ����ã�����0.2s���ӡ�1��λ���˶�����2��λ�ã�����������У������ɵ���͵������ɵıպϻ�·�Ĵ�ͨ����0.2Wb���ӵ�0.6Wb����
�����ʱ����ͨ����·�Ĵ�ͨ���ı仯������=��
�����ʱ���ڻ�·�еĸ�Ӧ�綯��E=��
����U�ν���������費�ƣ�������ĵ���R=5������5sʱ���ڵ��������������Ϊ4J�������ʱ���ڻ�·�еĸ�Ӧ����Ϊ��
���𰸡�0.4Wb��2V��0.4A
�������������ʱ����ͨ����·�Ĵ�ͨ���ı仯��Ϊ������=��2����1=0.6Wb��0.2Wb=0.4Wb
���ɷ����ڵ�Ÿ�Ӧ���ɵã�![]()
�۸��ݽ�������Ϊ��Q=I2Rt
�ã� ![]()
�𣺢����ʱ����ͨ����·�Ĵ�ͨ���ı仯������Ϊ0.4Wb��
�����ʱ���ڻ�·�еĸ�Ӧ�綯��E�Ĵ�СΪ2V��
�����ʱ���ڻ�·�еĸ�Ӧ����Ϊ0.4A��
�����㾫�������ڱ��⿼�����ζ��ɣ���Ҫ�˽���ζ���������һ������ĸ�Ӧ����������ж��������ֶ���ֻ�����ڵ����и�Ÿ����˶��������������������ֶ����ж�������ζ����ж������ܵó���ȷ�𰸣�