题目内容
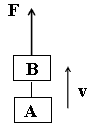
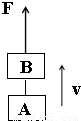
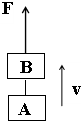 一起重机竖直吊起两个质量均为200kg的重物A和B,以4m/s的速度向上匀速运动.当物体A运动到距地面的高度为12m时,连接A、B间的绳子突然断裂,绳子断裂后,起重机的拉力保持不变,不计空气阻力,g取10m/s2,求:
一起重机竖直吊起两个质量均为200kg的重物A和B,以4m/s的速度向上匀速运动.当物体A运动到距地面的高度为12m时,连接A、B间的绳子突然断裂,绳子断裂后,起重机的拉力保持不变,不计空气阻力,g取10m/s2,求:(1)从绳子断裂到重物A落地所用的时间为多少?
(2)重物A落地时,重物B的速度大小为多少?
分析:(1)绳子断裂后重物A做竖直上抛运动,初速度为4m/s,将它的运动看成一种匀减速直线运动,由高度和初速度,即可由位移公式求得时间.
(2)绳子断裂后,B物匀加速上长,根据牛顿第二定律求出B运动的加速度.由速度公式VB=V0+at求其速度.
(2)绳子断裂后,B物匀加速上长,根据牛顿第二定律求出B运动的加速度.由速度公式VB=V0+at求其速度.
解答:解:(1)取竖直向下方向为正方向.绳子断裂后重物A做竖直上抛运动,将它的运动看成一种匀减速直线运动.
从断裂到落地处的位移为S=12m,加速度为a=g=10m/s2,初速度为v0=-4m/s
则有:S=v0t+
at2
代入数据:12=-4+5t2
解得:t=2s
(2)两物体一起匀速上升时:F=(mA+mB)g=2mg
B加速上升时:F-mg=ma
解得:a=10 m/s2
A落地时B的速度为:VB=V0+at
解得:VB=24m/s
答:
(1)从绳子断裂到重物A落地所用的时间为2s.
(2)重物A落地时,重物B的速度大小为24m/s.
从断裂到落地处的位移为S=12m,加速度为a=g=10m/s2,初速度为v0=-4m/s
则有:S=v0t+
| 1 |
| 2 |
代入数据:12=-4+5t2
解得:t=2s
(2)两物体一起匀速上升时:F=(mA+mB)g=2mg
B加速上升时:F-mg=ma
解得:a=10 m/s2
A落地时B的速度为:VB=V0+at
解得:VB=24m/s
答:
(1)从绳子断裂到重物A落地所用的时间为2s.
(2)重物A落地时,重物B的速度大小为24m/s.
点评:本题是脱钩问题,分析物体的运动情况,把握运动规律是关键,第2题,也可以根据动量守恒定律求解.

练习册系列答案
相关题目
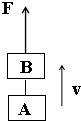 一起重机竖直吊起两个质量均为200kg的重物A和B,以4m/s的速度向上匀速运动.当物体A运动到距地面的高度为12m时,连接A、B间的绳子突然断裂,绳子断裂后,起重机的拉力保持不变,不计空气阻力,g取10m/s2,求:
一起重机竖直吊起两个质量均为200kg的重物A和B,以4m/s的速度向上匀速运动.当物体A运动到距地面的高度为12m时,连接A、B间的绳子突然断裂,绳子断裂后,起重机的拉力保持不变,不计空气阻力,g取10m/s2,求: