题目内容
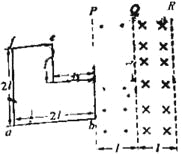
【题目】如图所示,两根互相平行的金属导轨MN、PQ水平放置,相距d=1m、且足够长、不计电阻。AC、BD区域光滑,其它区域粗糙且动摩擦因数μ=0.2,并在AB的左侧和CD的右侧存在着竖直向下的匀强磁场,磁感应强度B=2T。在导轨中央放置着两根质量均为m=1kg,电阻均为R=2Ω的金属棒a、b,用一锁定装置将一弹簧压缩在金属棒a、b之间(弹簧与a、b不栓连),此时弹簧具有的弹性势能E=9J。现解除锁定,当弹簧恢复原长时,a、b棒刚好进入磁场,且b棒向右运动x=0.8m后停止,g取10m/s2,求:
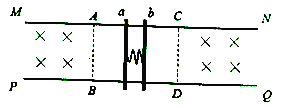
(1)a、b棒刚进入磁场时的速度大小;
(2)金属棒b刚进入磁场时的加速度大小
(3)整个运动过程中电路中产生的焦耳热。
【答案】(1)3m/s(2)8m/s2(3)5.8J
【解析】
对ab系统,所受的合外力为零,则动量守恒,根据动量守恒定律和能量关系列式求解速度;(2)当ab棒进入磁场后,两棒均切割磁感线,产生感生电动势串联,求解感应电流,根据牛顿第二定律求解b刚进入磁场时的加速度;(3)由能量守恒求解产生的热量.
(1)对ab系统,由动量守恒:0=mva-mvb
由能量关系:![]()
解得va=vb=3m/s
(2)当ab棒进入磁场后,两棒均切割磁感线,产生感生电动势串联,则有:Ea=Eb=Bdva=6V又:![]()
对b,由牛顿第二定律:BId+μmg=mab
解得ab=8m/s2
(3)由动量守恒可知,ab棒速率时刻相同,即两者移动相同距离后停止,则对系统,由能量守恒:EP=2μmgx+Q
解得Q=5.8J

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目