题目内容
4.如图所示是某同学探究“加速度与力的关系”的实验装置,他在固定于桌面上的光滑导轨上安装了一个光电门传感器B,小车上固定一挡光片,已知挡光片的宽度为d,小车用细线绕过导轨左端的定滑轮与力传感器C相连,传感器下方悬挂钩码,每次小车都从A处由静止释放.(不计导轨及滑轮的摩擦)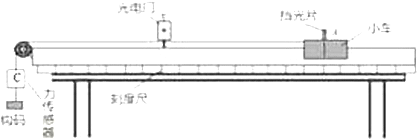
(1)实验时,将小车从A位置由静止释放,由光电门传感器测出挡光片通过光电门B的时间t,则小车通过光电门时的速度为$\frac{d}{t}$,若要得到小车的加速度,还需要测量的物理量是AB间的距离L.
(2)下列不必要的实验要求是A.
A、应使小车质量远大于钩码和力传感器的总质量
B、应使A位置与光电门传感器间的距离适当大些
C、应将力传感器和光电门传感器都通过数据采集器连接到计算机上
D、应使细线与导轨平行
(3)改变钩码质量,测出对应的力传感器的示数F和挡光片通过光电门的时间t,通过描点做出线性图象,研究小车的加速度与力的关系,处理数据时应作出$\frac{1}{{t}^{2}}$-F图象(选填“t2-F”、“$\frac{1}{t}$-F”或“$\frac{1}{{t}^{2}}$-F”),图象斜率k与挡光片的宽度d的关系为k∝$\frac{1}{{d}^{2}}$.
分析 滑块经过光电门时的瞬时速度可近似认为是滑块经过光电门的平均速度.根据运动学公式解答.用细线拉力表示合力,要考虑摩擦力的影响;最后根据牛顿第二定律与运动学公式结合,从而确定选取什么样的图象.
解答 解:(1)实验时,将滑块从A位置由静止释放,由数字计时器读出遮光条通过光电门B的时间t,滑块经过光电门时的瞬时速度可近似认为是滑块经过光电门的平均速度,即v=$\frac{d}{t}$;
根据运动学公式得若要得到滑块的加速度,还需要测量的物理量是释放点距光电门的距离L,即AB间的距离L;
(2)A、拉力是直接通过传感器测量的,故与小车质量和钩码质量大小关系无关,故A错误;
B、应使A位置与光电门间的距离适当大些,有利于减小误差,故B正确;
C、应将力传感器和光电门传感器都通过数据采集器连接到计算机上,故C正确;
D、要保持拉线方向与导轨平面平行,拉力才等于合力,故D正确;
本题选择错误的,故选:A.
(3)由题意可知,该实验中保持小车质量M不变,因此有:v2=2as,
因v=$\frac{d}{t}$,
由牛顿第二定律,a=$\frac{F}{M}$,
则有:$\frac{{d}^{2}}{{t}^{2}}=2\frac{F}{M}L$
即为$\frac{1}{{t}^{2}}=\frac{2L}{M{d}^{2}}F$
所以研究滑块的加速度与力的关系,处理数据时应作出$\frac{1}{{t}^{2}}$-F图象.
因此图象斜率k=$\frac{2L}{M{d}^{2}}$,即有:k∝$\frac{1}{{d}^{2}}$.
故答案为:(1)$\frac{d}{t}$;AB间的距离L;(2)A;(3)$\frac{1}{{t}^{2}}$-F;k∝$\frac{1}{{d}^{2}}$
点评 处理实验时一定要找出实验原理,根据实验原理我们可以寻找需要测量的物理量和需要注意的事项,掌握牛顿第二定律与运动学公式的应用.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案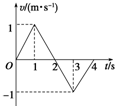
| A. | 物体在第1 s末运动方向发生变化 | |
| B. | 物体在第2 s末运动方向发生变化 | |
| C. | 物体在第2 s内和第3 s内的加速度方向相反 | |
| D. | 物体在4 s末离出发点最远 |
 如图所示,不计质量的光滑小滑轮用细绳悬挂于墙上O点,跨过滑轮的细绳连接物块A、B,A、B都处于静止状态,现将物块B移至C点后,A、B仍保持静止,下列说法中正确的是( )
如图所示,不计质量的光滑小滑轮用细绳悬挂于墙上O点,跨过滑轮的细绳连接物块A、B,A、B都处于静止状态,现将物块B移至C点后,A、B仍保持静止,下列说法中正确的是( )| A. | β角将大于α角 | B. | 悬于墙上的绳所受拉力不变 | ||
| C. | B与水平面间的摩擦力减小 | D. | 地面对B的弹力增大 |
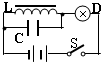 如图所示的电路中,L是自感系数很大的、用铜导线绕制成的理想线圈.开关S原来是闭合的,且小灯泡D正常发光,当开关S断开时( )
如图所示的电路中,L是自感系数很大的、用铜导线绕制成的理想线圈.开关S原来是闭合的,且小灯泡D正常发光,当开关S断开时( )| A. | 灯泡D立即熄灭 | |
| B. | L中电流立即反向 | |
| C. | LC电路将发生电磁振荡,且刚断开S时电场能最大 | |
| D. | 刚断开S后,电容器开始充电,磁场能开始向电场能转化 |
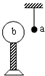 绝缘细线上端固定,下端挂一轻质小球a,a的表面镀有铝膜.在a的近旁有一绝缘金属球b,开始时,a、b都不带电,如图所示,现使b带正电,则( )
绝缘细线上端固定,下端挂一轻质小球a,a的表面镀有铝膜.在a的近旁有一绝缘金属球b,开始时,a、b都不带电,如图所示,现使b带正电,则( )| A. | b将吸引a,吸住后不放开 | B. | b立即把a排斥开 | ||
| C. | a、b之间不发生相互作用 | D. | b先吸引a,接触后又把a排斥开 |
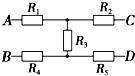
| A. | 若UAB=140V,C、D端开路,UCD=84V | B. | 若UAB=140V,C、D端开路,UCD=140V | ||
| C. | 若UCD=104V,A、B端开路,UAB=84V | D. | 若UCD=104V,A、B端开路,UAB=60V |
 细杆AB长L,两端分别约束在x、y轴上运动
细杆AB长L,两端分别约束在x、y轴上运动
 如图所示,物体A放在足够长的木板B上,木板B静止于水平面.t=0时,电动机通过水平细绳以恒力F拉木板B,使它做初速度为零,加速度aB=4.0m/s2的匀加速直线运动.已知A的质量mA和B的质量mB均为2.0kg,A、B之间的动摩擦因数μ1=0.2,B与水平面之间的动摩擦因数μ2=0.4,最大静摩擦力与滑动摩擦力大小视为相等,重力加速度g取10m/s2.求:
如图所示,物体A放在足够长的木板B上,木板B静止于水平面.t=0时,电动机通过水平细绳以恒力F拉木板B,使它做初速度为零,加速度aB=4.0m/s2的匀加速直线运动.已知A的质量mA和B的质量mB均为2.0kg,A、B之间的动摩擦因数μ1=0.2,B与水平面之间的动摩擦因数μ2=0.4,最大静摩擦力与滑动摩擦力大小视为相等,重力加速度g取10m/s2.求: