��Ŀ����
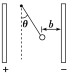
����Ŀ��ijͬѧ�����һ��ŵ���װ�ã���ͼ��ʾ����ˮƽ���Ϲ̶������㹻����ƽ�н������죬������ΪL��1m������ĵ��費�ƣ����촦����ֱ���Ÿ�Ӧǿ�ȴ�СΪB��2T����ǿ�ų���ͼ������֮������δ�����������ӵ���ĵ�Դ�綯��ΪE��40V���������ĵ���ΪC��1F��С���ײ��̶�һ������ǰ��ƽ�롢�߳�ΪL�������ε��ѵ����߿��߿�ǰ�����ߵĵ����ΪR��0.2��������ߵ��費�����뵼��Ӵ����á�С�����߿��������Ϊm��lkg����ʼС�����ھ�ֹ״̬���ֽ�����S��1��ʹ��������ȫ��磬�ٽ�S����2��С����ǰ�����˶�����С����ʼ�����˶�ʱ��������S�λ�1�����С�������ų�������С�����˶������е�Ħ������

(1)�ų��ķ����С����ʼ�˶�ʱ�ļ��ٶȴ�Сa��
(2)С���ڹ���ϴﵽ����ʱ���ٶȴ�Сv1��
(3)С�����ų��������߿��в����Ľ�����Q��
���𰸡�(1)�ų��ķ����С����ʼ�˶�ʱ�ļ��ٶȴ�С800m/s2��
(2)С���ڹ���ϴﵽ����ʱ���ٶȴ�С16m/s��
(3)С�����ų��������߿��в����Ľ�����110J��
��������
(1)�ų�����ֱˮƽ�����ϣ�
С���ڵ������˶������У������貢�������У� ��
��
С����ʼ�˶��ļ��ٶ�Ϊ��![]() ��
��
�������ݣ���ã�a��800m/s2��
(2)�����ɺ����У�q��CE
�ŵ���ٹ����У�Ӧ�ö������������У�BIL��t��B��qL��mv1��0
����q��q��q1
�����˶�ʱ�����������˵�ѹ��С���и�����ĵ��Ʋ���ȣ����У�![]()
����ʽ��������ã�![]()
�������ݣ���ã�v1��16m/s
(3)С�����ų��Ĺ����У��������˶����ɶ������������У���Ft����BILt��mv2��mv1
С���������贮����![]()
��L��vt
����![]()
�������ݣ���ã�v2��6m/s
����С�������ų������в����Ľ����ȣ�Ϊ![]()
�������ݣ���ã�Q��110J