题目内容
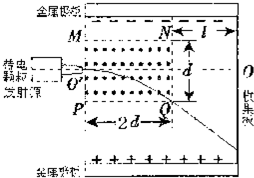 有人设计了一种带电颗粒的速率分选装置,其原理如题23图所示.两带电金属板间有匀强电场,方向竖直向上,其中PQNM矩形区域内还有方向垂直纸面向外的匀强磁场.一束比荷(电荷量与质量之比)均为l/k的带正电颗粒,以不同的速率沿着磁场区域的中心线O'O进入两金属板之间,其中速率为V.的颗粒刚好从Q点处离开磁场,然后做匀速直线运动到达收集板.重力加速度为g,PQ=2d,NQ=d,收集板与NQ的距离为l,不计颗粒间相互作用,求
有人设计了一种带电颗粒的速率分选装置,其原理如题23图所示.两带电金属板间有匀强电场,方向竖直向上,其中PQNM矩形区域内还有方向垂直纸面向外的匀强磁场.一束比荷(电荷量与质量之比)均为l/k的带正电颗粒,以不同的速率沿着磁场区域的中心线O'O进入两金属板之间,其中速率为V.的颗粒刚好从Q点处离开磁场,然后做匀速直线运动到达收集板.重力加速度为g,PQ=2d,NQ=d,收集板与NQ的距离为l,不计颗粒间相互作用,求(1)电场强度E的大小
(2)磁感应强度B的大小.
分析:(1)根据电场力与重力平衡,及粒子的比荷,即可求解;
(2)根据粒子做匀速圆周运动,洛伦兹力提供向心力,与几何关系相结合,即可求解.
(2)根据粒子做匀速圆周运动,洛伦兹力提供向心力,与几何关系相结合,即可求解.
解答:解: (1)设带电颗粒的电量为q,质量为m,因带电颗粒做匀速运动,
(1)设带电颗粒的电量为q,质量为m,因带电颗粒做匀速运动,
故 有
qE=mg
将
=
代入得:E=kg
(2)如答图所示,因带电颗粒在矩形空间PQNM中做匀速圆周
运动,有
qv0B=m
由几何关系得:R2=(2d)2+(R-
)2
得 B=
答:(1)电场强度E的大小为kg;
(2)磁感应强度B的大小为
.
 (1)设带电颗粒的电量为q,质量为m,因带电颗粒做匀速运动,
(1)设带电颗粒的电量为q,质量为m,因带电颗粒做匀速运动,故 有
qE=mg
将
| q |
| m |
| 1 |
| k |
代入得:E=kg
(2)如答图所示,因带电颗粒在矩形空间PQNM中做匀速圆周
运动,有
qv0B=m
| ||
| R |
由几何关系得:R2=(2d)2+(R-
| d |
| 2 |
得 B=
| 4kv0 |
| 17d |
答:(1)电场强度E的大小为kg;
(2)磁感应强度B的大小为
| 4kv0 |
| 17d |
点评:考查物体受力平衡条件,并由牛顿第二定律与几何关系相综合来解,粒子做匀速圆周运动情况.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
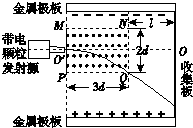 有人设计了一种带电颗粒的速率分选装置,其原理如图所示,两带电金属板间有匀强电场,方向竖直向上,其中PQNM矩形区域内还有方向垂直纸面向外的匀强磁场.一束比荷(电荷量与质量之比)均为
有人设计了一种带电颗粒的速率分选装置,其原理如图所示,两带电金属板间有匀强电场,方向竖直向上,其中PQNM矩形区域内还有方向垂直纸面向外的匀强磁场.一束比荷(电荷量与质量之比)均为 的带正电颗粒,以不同的速率沿着磁场区域的水平中心线O’O进入两金属板之间,其中速率为v0的颗粒刚好从Q点处离开磁场,然后做匀速直线运动到达收集板。重力加速度为g,PQ=3d,NQ=2d,收集板与NQ的距离为l,不计颗粒间相互作用。求
的带正电颗粒,以不同的速率沿着磁场区域的水平中心线O’O进入两金属板之间,其中速率为v0的颗粒刚好从Q点处离开磁场,然后做匀速直线运动到达收集板。重力加速度为g,PQ=3d,NQ=2d,收集板与NQ的距离为l,不计颗粒间相互作用。求
 的带正电颗粒,以不同的速率沿着磁场区域的水平中心线O’O进入两金属板之间,其中速率为v0的颗粒刚好从Q点处离开磁场,然后做匀速直线运动到达收集板。重力加速度为g,PQ=3d,NQ=2d,收集板与NQ的距离为l,不计颗粒间相互作用。求
的带正电颗粒,以不同的速率沿着磁场区域的水平中心线O’O进入两金属板之间,其中速率为v0的颗粒刚好从Q点处离开磁场,然后做匀速直线运动到达收集板。重力加速度为g,PQ=3d,NQ=2d,收集板与NQ的距离为l,不计颗粒间相互作用。求
 的带正电颗粒,以不同的速率沿着磁场区域的水平中心线为O′O进入两金属板之间,其中速率为v的颗粒刚好从Q点处离开磁场,然后做匀速直线运动到达收集板.重力加速度为g,PQ=3d,NQ=2d,收集板与NQ的距离为l,不计颗粒间相互作用.求:
的带正电颗粒,以不同的速率沿着磁场区域的水平中心线为O′O进入两金属板之间,其中速率为v的颗粒刚好从Q点处离开磁场,然后做匀速直线运动到达收集板.重力加速度为g,PQ=3d,NQ=2d,收集板与NQ的距离为l,不计颗粒间相互作用.求: