题目内容
如图所示,一砂袋用无弹性轻细绳悬于O点.开始时砂袋处于静止状态,此后用弹丸以水平速度击中砂袋后均未穿出。第一次弹丸的速度为v0,打入砂袋后二者共同摆动的最大摆角为θ(θ<90°),当其第一次返回图示位置时,第二粒弹丸以另一水平速度v又击中砂袋,使砂袋向右摆动且最大摆角仍为θ.若弹丸质量均为m,砂袋质量为5m,弹丸和砂袋形状大小忽略不计,求:两粒弹丸的水平速度之比 为多少?
为多少?
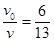
解析试题分析:弹丸击中砂袋瞬间,系统水平方向不受外力,动量守恒,设碰后弹丸和砂袋的共同速度为v1,细绳长为L,根据动量守恒定律有mv0=(m+5m)v1,
砂袋摆动过程中只有重力做功,机械能守恒,所以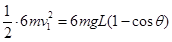
设第二粒弹丸击中砂袋后弹丸和砂袋的共同速度为v2,同理有:mv-(m+5m)v1=(m+6m)v2
联解上述方程得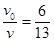
考点:动量守恒定律及机械能守恒定律.

练习册系列答案
相关题目
在下列所描述的运动过程中,若物体所受的空气阻力均可忽略不计,则机械能守恒的是 ( )
| A.小孩沿滑梯匀速滑下 |
| B.电梯中的货物随电梯一起匀速下降 |
| C.发射过程中的火箭加速上升 |
| D.被投掷出的铅球在空中运动 |
小船在200m宽的河中过河,水流速度是4m/s,船在静水中的航速是5m/s,则下列判断正确的是 ( )
| A.小船过河所需的最短时间是40s |
| B.要使小船过河的位移最短,船头应始终正对着对岸 |
| C.要使小船过河的位移最短,过河所需的时间是50s |
| D.如果水流速度增大为6m/s,小船过河所需的最短时间将增大 |
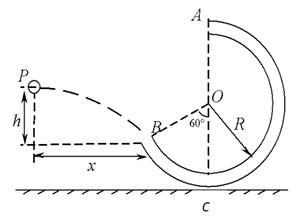
 的斜面,倾角为60°,其顶端与弧形轨道末端相接,斜面正中间有一竖直放置的直杆,现让质量为1Kg的物块从弧形轨道的顶端由静止开始滑下,物块离开弧形轨道后刚好能从直杆的顶端通过,重力加速度取10m/s2,求:
的斜面,倾角为60°,其顶端与弧形轨道末端相接,斜面正中间有一竖直放置的直杆,现让质量为1Kg的物块从弧形轨道的顶端由静止开始滑下,物块离开弧形轨道后刚好能从直杆的顶端通过,重力加速度取10m/s2,求:


 )
)