题目内容
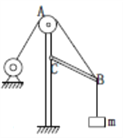
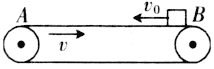
【题目】如图所示，abcd为一矩形金属线框，其中ab＝cd＝L，ab边接有定值电阻R， cd边的质量为m，其它部分的电阻和质量均不计，整个装置用两根绝缘轻弹簧悬挂起来。线框下方处在磁感应强度大小为B的匀强磁场中，磁场方向垂直于纸面向里。初始时刻，使两弹簧处于自然长度，且给线框一竖直向下的初速度v 0，当cd边第一次运动至最下端的过程中，R产生的电热为Q，此过程cd边始终未离开磁场，已知重力加速度大小为g，下列说法中正确的是（ ）
A. 初始时刻cd边所受安培力的大小为
B. 线框中产生的最大感应电流可能为
C. cd边第一次到达最下端的时刻，两根弹簧具有的弹性势能总量大于
D. 在cd边反复运动过程中，R中产生的电热最多为
【答案】BC
【解析】
对cd棒受力分析，确定棒的运动形式，求解最大速度，再由E=BLv和I=E/R及F=BIL分别确定电流和安培力的大小，再由能量守恒定律确定能量关系．
初始时刻时，棒的速度为v0，由E=BLv=BLv0，再由I=E/R及F=BIL，得cd边所受安培力的大小 F=
，故A错误；cd棒开始运动后，对cd棒受力分析，受重力和安培力及弹簧弹力，无法确定重力和安培力的关系，当重力大于安培力时，由mg-
-kx=ma，合力方向向下，可知导体棒可能先做加速度减小的加速运动，故v0不是速度的最大值，产生的感应电动势不是最大，感应电流不是最大，当重力小于安培力时，由+kx-mg=ma，合力方向向上，可知导体棒可能先做加速度减小的减速运动，速度v0为最大值，线框中产生的最大感应电流大于等于
，故B正确；cd边第一次到达最下端的时刻，由能量守恒定律可知，导体棒的动能和减少的重力势能转化为焦耳热及弹簧的弹性势能，即：mgh+
=Ep+Q，所以：EP-mgh=-Q，故弹簧弹性势能大于-Q，故C正确；在cd边反复运动过程中，可知最后棒静止在初始位置的下方，设两弹簧弹簧并联后的劲度系数为k，由mg=kx得：x=
，由能量守恒定律可知，导体棒的动能和减少的重力势能转化为焦耳热及弹簧的弹性势能，弹性势能EP=
kx2=
，减少的重力势能为：mgh=
，因重力势能大于弹性势能，根据mgh+mv02=Ep+Q，可知热量应大于mv02，故D错误；故选BC。
