题目内容
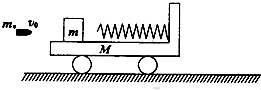 如图所示,在光滑的水平面上有一质量为M=1kg的小车,车上固定着一处于自然长度的轻质弹簧,将质量为m=0.98kg的光滑木块放在小车上,整个装置处于静止,现有一质量为m0=0.02kg的子弹以某一水平速度射向木块且留在木块内(子弹和木块作用过程时间极短,木块与弹簧、小车相互作用的过程中无机械能损失),最后木块离开小车做自由落体运动,小车以速度υ=2m/s匀速运动,求:
如图所示,在光滑的水平面上有一质量为M=1kg的小车,车上固定着一处于自然长度的轻质弹簧,将质量为m=0.98kg的光滑木块放在小车上,整个装置处于静止,现有一质量为m0=0.02kg的子弹以某一水平速度射向木块且留在木块内(子弹和木块作用过程时间极短,木块与弹簧、小车相互作用的过程中无机械能损失),最后木块离开小车做自由落体运动,小车以速度υ=2m/s匀速运动,求:(1)子弹的初速度 υ0.
(2)在木块压缩弹簧过程中,弹簧的最大弹性势能.
分析:1、子弹,木块与小车作为系统,整个过程动量守恒,列出等式求解.
2、木块与子弹碰撞,时间极短,动量守恒列出等式,然后弹簧开始压缩,当车子,木块和子弹在同一速度时,弹性势能最大,
根据动量守恒求出共同速度,再根据能量守恒定律求解.
2、木块与子弹碰撞,时间极短,动量守恒列出等式,然后弹簧开始压缩,当车子,木块和子弹在同一速度时,弹性势能最大,
根据动量守恒求出共同速度,再根据能量守恒定律求解.
解答:解:(1)最后木块离开小车做自由落体运动,即水平方向的速度为0.
子弹,木块与小车作为系统,整个过程动量守恒,规定子弹初速度方向为正方向,列出等式:
m0υ0+0=Mv+0
解得:v=100m/s
(2)木块与子弹碰撞,时间极短,由动量守恒列出等式,
m0υ0+0=(m0+m)V1,
解得:V1=2m/s
然后弹簧开始压缩,当车子,木块和子弹在同一速度时,弹性势能最大,
根据动量守恒得:
(m0+m)V1=(M+m+m0)V2,
解得:V2=1m/s
根据能量守恒定律得:
Ep=
(m0+m)
-
(M+m+m0)
解得:Ep=1J
答:(1)子弹的初速度是100m/s.
(2)在木块压缩弹簧过程中,弹簧的最大弹性势能是1J.
子弹,木块与小车作为系统,整个过程动量守恒,规定子弹初速度方向为正方向,列出等式:
m0υ0+0=Mv+0
解得:v=100m/s
(2)木块与子弹碰撞,时间极短,由动量守恒列出等式,
m0υ0+0=(m0+m)V1,
解得:V1=2m/s
然后弹簧开始压缩,当车子,木块和子弹在同一速度时,弹性势能最大,
根据动量守恒得:
(m0+m)V1=(M+m+m0)V2,
解得:V2=1m/s
根据能量守恒定律得:
Ep=
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
解得:Ep=1J
答:(1)子弹的初速度是100m/s.
(2)在木块压缩弹簧过程中,弹簧的最大弹性势能是1J.
点评:本题是系统的动量守恒和能量守恒问题,关键要分析过程,正确选择研究对象,再根据两大守恒求解.

练习册系列答案
相关题目
 如图所示,在光滑的水平板的中央有一光滑的小孔,用不可伸长的轻绳穿过小孔,绳的两端分别挂上小球C和物体B,在B的下端再挂一重物A,现使小球C在水平板上以小孔为圆心做匀速圆周运动,稳定时圆周运动的半径为R,现剪断连接A、B的绳子,稳定后,小球以另一半径在水平面上做匀速圆周运动,则下列说法正确的是( )
如图所示,在光滑的水平板的中央有一光滑的小孔,用不可伸长的轻绳穿过小孔,绳的两端分别挂上小球C和物体B,在B的下端再挂一重物A,现使小球C在水平板上以小孔为圆心做匀速圆周运动,稳定时圆周运动的半径为R,现剪断连接A、B的绳子,稳定后,小球以另一半径在水平面上做匀速圆周运动,则下列说法正确的是( ) 如图所示,在光滑的水平板的中央有一光滑的小孔,一根不可伸长的轻绳穿过小孔.绳的两端分别拴有一小球C和一质量为m的物体B,在物体B的下端还悬挂有一质量为3m的物体A.使小球C在水平板上以小孔为圆心做匀速圆周运动,稳定时,圆周运动的半径为R.现剪断连接A、B的绳子,稳定后,小球以2R的半径在水平面上做匀速圆周运动,则下列说法正确的( )
如图所示,在光滑的水平板的中央有一光滑的小孔,一根不可伸长的轻绳穿过小孔.绳的两端分别拴有一小球C和一质量为m的物体B,在物体B的下端还悬挂有一质量为3m的物体A.使小球C在水平板上以小孔为圆心做匀速圆周运动,稳定时,圆周运动的半径为R.现剪断连接A、B的绳子,稳定后,小球以2R的半径在水平面上做匀速圆周运动,则下列说法正确的( ) 如图所示,在光滑的水平板的中央有一光滑的小孔,用不可伸长的轻绳穿过小孔,绳的两端分别栓上一小球C和一物体B,在B的下端再悬挂一重物A,现使小球C在水平板上以小孔为圆心做匀速圆周运动,稳定时,圆周运动半径为R.现剪断连接AB的绳子,稳定后,小球以另一半径在水平面上做匀速圆周运动,则下列说法正确的是( )
如图所示,在光滑的水平板的中央有一光滑的小孔,用不可伸长的轻绳穿过小孔,绳的两端分别栓上一小球C和一物体B,在B的下端再悬挂一重物A,现使小球C在水平板上以小孔为圆心做匀速圆周运动,稳定时,圆周运动半径为R.现剪断连接AB的绳子,稳定后,小球以另一半径在水平面上做匀速圆周运动,则下列说法正确的是( )
