题目内容
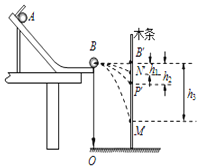
【题目】如图所示，质量为2kg的木板M放置在足够大光滑水平面上，其右端固定一轻质刚性竖直挡板，对外最大弹力为4N，质量为1kg的可视为质点物块m恰好与竖直挡板接触，已知M、m间动摩擦因数μ=0.5，假设最大静摩擦力等于滑动摩擦力。初始两物体均静止，某时刻开始M受水平向左力F作用，F与M位移关系为F=3+0.5x，重力加速度
，关于M、m的运动，下列表述正确的是
A. 当F刚作用时，竖直挡板对m就有弹力作用
B. m的最大加速度为
C. 当M运动位移为24m过程中，F所做的功为216J
D. m获得的最大速度无法求解
【答案】BC
【解析】当F刚作用时，F=3N，把M、m看成一个整体，由牛顿第一定律： 
，代入数据解得： 
，对m隔离分析： 
，m所受的最大静摩擦力为： 
，可见m所受的静摩擦力可以提供m的合外力，所以竖直挡板对m无弹力作用，故A错误；当m受到向左的最大静摩擦力和挡板的弹力达到最大时，m的加速度有最大值，由牛顿第二定律： 
，代入数据解得： 
，故B正确；外力F随位移成线性变化，当x=0时F=3N，当x=24时F=15N，作出F-x图像，可知图线与坐标轴所围的梯形面积即为所做的功： 
，故C正确；当竖直挡板对m的弹力达到4N时，m的速度有最大值，对m有： 
，代入数据解得： 
，此时的外力为
，由此可得运动的位移为： 
，那么F在该过程中做的功为： 
，由动能定理： 
，联立解得： 
，故D错误。所以BC正确，AD错误。
练习册系列答案
相关题目
