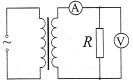
题目内容
【题目】如图所示,一辆平板小车静止在水平地面上,小车的质量M=3.0kg,平板车长度L=1.0m,平板车的上表面距离店面的高度H=0.8m。某时刻,一个质量m=1.0kg的小物块(可视为质点)以![]() 的水平速度滑上小车的左端,与此同时相对小车施加一个F=15N的水平向右的恒力。物块与小车之间的动摩擦因数
的水平速度滑上小车的左端,与此同时相对小车施加一个F=15N的水平向右的恒力。物块与小车之间的动摩擦因数![]() ,不计小车与地面间的摩擦。重力加速度g取
,不计小车与地面间的摩擦。重力加速度g取![]() 。求:
。求:
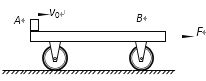
(1)物块相对小车滑行的最大距离;
(2)物块落地时,物块与小车左端之间的水平距离。
【答案】(1)0.5m;(2)0.8m
【解析】
(1)假设物块不会从小车右端滑出,设从物块滑上小车,经过时间t1后,物块与小车达到共同速度v1,这段时间内物块做匀减速运动,小车做匀加速直线运动.
根据牛顿第二定律得,物块的加速度
![]()
方向向左.
小车的加速度
![]() =6m/s2
=6m/s2
方向向右.
根据
v1=v0-a物1t1,=a车1t1,
代入数据解得:
![]()
v1=2.0m/s.
则
![]() ,
,
![]() ,
,
物块相对小车滑行的距离
△x1=x物1-x车1=0.5m,
因为△x1<L,所以物块没有从小车右端滑出,此后物块的速度小于小车的速度,将相对小车向左端运动,所以物块相对小车滑行的最大距离△x1=0.5m.
(2)物块相对小车向左端滑动的过程中,物块和小车都做匀加速直线运动,根据牛顿第二定律得,
物块的加速度
![]()
方向向右.
小车的加速度
![]() =4m/s2
=4m/s2
方向向右.
设再经过时间t2,物块运动到小车的左端,这段时间内,物块和小车的位移分别为
![]()
![]()
由因为
x车2-x物2=△x1,
代入数据解得
t2=1.0s,
此时
v物2=v1+a物2t2=5m/s,
v车2=v1+a车2t2=6m/s,
此时物块从小车左端滑行,做平抛运动,小车做匀加速直线运动,根据牛顿第二定律,
小车的加速度
![]()
设物块做平抛运动的时间为t3,
H=![]()
解得
t3=0.4s,
这段时间内物块在水平方向的位移
x物3=v物2t3=5×0.4m=2m,
小车的位移
![]() ,
,
代入数据解得
x车3=2.8m
所以物块落地时,物块与小车左端之间的水平距离
△x=x车3-x物3=2.8-2m=0.8m.

 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案