Question

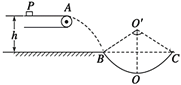
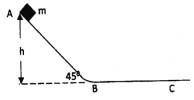
【题目】如图所示，AB为斜轨道，与水平方向成450角，BC为水平轨道，两轨道在B处通过一段小圆弧相连接，一质量为m的小物块，自轨道的 A处从静止开始沿轨道下滑，最后停在轨道上的C点，己知A点高h，物块与轨道间的滑动摩擦系数为，求：

（1）在整个滑动过程中摩擦力所做的功.

（2）物块沿轨道AB段滑动时间t1与沿轨道BC段滑动时间t2之比值tl/ t2.

（3）使物块匀速地、缓慢地沿原路回到A点所需做的功.

Answer 1

【答案】（1）﹣mgh（2） （3）2mgh

【解析】

根据动能定理求出整个过程中摩擦力做功的大小根据牛顿第二定律求出物块在斜面上和在水平面上的加速度大小之比，从而求出滑动的时间之比；根据动能定理，抓住动能变化量为零，求出沿原路回到A点所需做的功．

（1）对全过程运用动能定理得，则；

（2）根据牛顿第二定律得，

物块在斜面上的加速度；

物块在水平面上的加速度

根据知，物块沿轨道AB段滑动时间与沿轨道BC段滑动时间之比；
（3）根据动能定理得，解得。